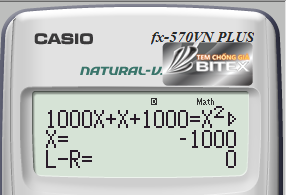BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải hệ phương trình trên tập số thực
- 08/11/2017
- 206 lượt xem
Bài toán: Giải hệ phương trình sau trên tập số thực:
[latex]\left\{\begin{matrix} xy+x+y=x^{2}-2y^{2} & & \\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y & & \end{matrix}\right.[/latex]Bài giải:Điều kiện [latex]x\geqslant 1, y\geqslant 0[/latex]
Từ phương trình thứ nhất của hệ cho [latex]y=1000[/latex], nhập phương trình ẩn chính là [latex]x[/latex], nhấn tổ hợp phím SHIFT+CALC+= máy cho kết quả [latex]x=-1000[/latex]
Như vậy phương trình thứ nhất của hệ chứa nhân tử [latex]\left ( x+y \right )[/latex]
Phương trình thứ nhất của hệ đã cho tương đương;
[latex]\left ( x+y \right )\left ( x-2y-1 \right )=0[/latex]Thay [latex]x=-y[/latex] vào phương trình thứ hai thấy rằng phương trình vô nghiệm do vế trái không âm và vế phải nhỏ hơn 0.
Với [latex]x=2y+1[/latex] , thay vào phương trình thứ hai ta được
[latex]\left ( y+1 \right )\left ( \sqrt{2y}-2 \right )=0\Leftrightarrow y=2[/latex]Vậy nghiệm của hệ phương trình đã cho là [latex]\left ( x,y \right )=\left ( 5;2 \right )[/latex]
Chia sẻ
About casiobitex
