Dùng thước, thước đo góc và compa vẽ ký hiệu Euro (dành cho HS lớp 10)

Trước hết ta quan sát bản thiết kế

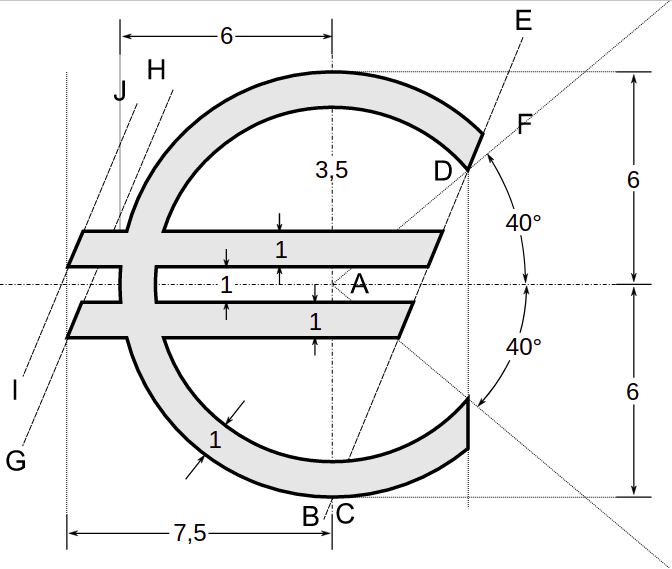
Đối với học sinh lớp 10 các em không lấy trung điểm của đoạn bán kính phải của đường tròn  nhỏ. Vẽ một tia $At$ hợp với chiều dương của truc hoành một góc $40^\circ$ cắt đường tròn  nhỏ tại $D$. Vẽ đường thẳng  $BD$  cắt hai đường tròn  lần lượt tại $D$ và $F$ như trong bản thiết kế. Các chi tiết còn lại thực hiện như ở lớp 9.

Trong bài viết này chúng ta sẽ tính chi tiết các điểm với toạ độ cực, tức là xác định góc tạo bởi chiều dương của truc hoành với vectơ có gốc là gốc toạ độ $A$ và có ngọn là điểm đó. Việc tính toán này phục vụ cho việc vẽ biểu tượng này bằng $\rm \LaTeX$. Ở đây chúng tôi chỉ tính góc $\varphi$ tạo bởi vectơ $\overrightarrow{AF}$ với chiều dương của trục hoành, các góc khác chỉ công bố kết quả 🙂

Ta thấy ngay toạ độ điểm $D$ là $D(5\cos40^\circ, 5\sin 40^\circ)$.

Phương trình đường thẳng  $BD$ là $y=kx-6$ với $k=\dfrac{y_D-y_B}{x_D-x_B}=\dfrac{5\sin 40^\circ +6}{5\cos 40^\circ}$

Giao điểm với đường tròn  lớn xác định bởi phương trình  hoành độ giao điểm $$(1+k^2)x^2-12kx=0$$ loại $x=0$ ta có hoành độ điểm $D$ là $x=\dfrac{12k}{1+k^2}$, tung độ $y=kx-6=\dfrac{6(k^2-1)}{1+k^2}$.

Suy ra $\tan\varphi=\dfrac{y}{x}=\dfrac12.\dfrac{k^2-1}{k}=\dfrac12.\dfrac{50\sin^240^\circ+60\sin 40^\circ+11}{5\cos 40^\circ (5\sin 40^\circ+6)}=\dfrac{60\sin 40^\circ -25\sin 10^\circ +36}{10\cos 40^\circ(5\sin 40^\circ+6)}$.

Tóm lại $$\varphi =\arctan\left[\dfrac{60\sin 40^\circ -25\sin 10^\circ +36}{10\cos 40^\circ(5\sin 40^\circ+6)}\right]$$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.