Có một hình vuông cạnh $10 cm$ chứa một hình tròn tiếp xúc với 4 cạnh của hình vuông. Tính diện tích phần tô đậm trong hình vẽ dưới đây (phần giao của hình tròn này với hai cung tròn tâm là hai đỉnh hình vuông bán kính $10 cm$).

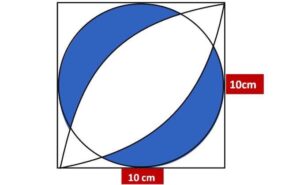
Liệu bạn có giải được bài toán này với kiến thức từ lớp 11 trở xuống không?

(Tham khảo thông tin từ VnExpress,Nguồn đề: link ).

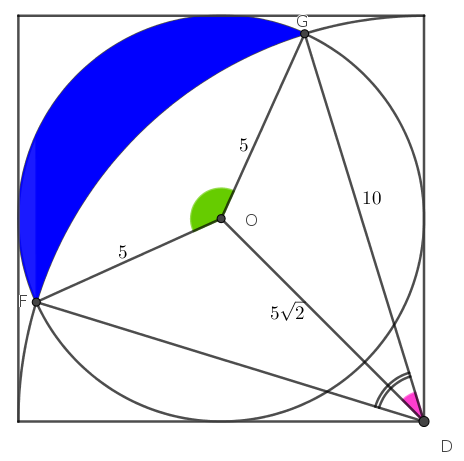
Độ dài các cạnh được ghi trên hình vẽ.

Gọi $S_1$ là diện tích hình quạt tròn $OFG$ của hình tròn tâm $O$.

$S_2$ là diện tích hình quạt tròn $DFG$ của hình tròn tâm $D$.

Diện tích hình quạt tròn cho bởi công thức $$S_{\text{quạt}}=\dfrac12R^2\theta$$

trong đó $\theta$ là góc xòe của cái quạt.

$S_3$ là diện tích tam giác $DOG$.

Diện tích cần tìm bằng $S=2(S_1-(S_2-2S_3))$.

$S_3$ được tính bằng công thức Hê-rông

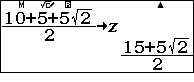
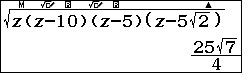
$\sin \widehat{ODG}=\dfrac{2S_{ODG}}{DO.DG}=\dfrac{\sqrt{14}}{8} \Rightarrow \cos \widehat{FDG}=1-2\sin^2\widehat{ODG}=$ Trong tam giác $DFG$ ta có $FG^2=DG^2+DF^2-2.DF.DG.\cos \widehat{ODG}=$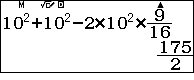

Suy ra $\cos \widehat{FOG}=\dfrac{OG^2+OF^2-FG^2}{2.OG.OF}=$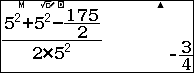

Vậy: $$S=2\left[\dfrac{25}{2}\arccos\left(-\dfrac34\right)-\left(50\arccos\dfrac{9}{16}-\dfrac{25\sqrt7}{2}\right)\right]$$

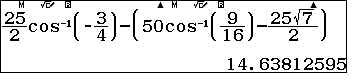
Tóm lại

$\approx$

KIỂM TRA KẾT QUẢ TÍNH

1. Bằng Geogebra



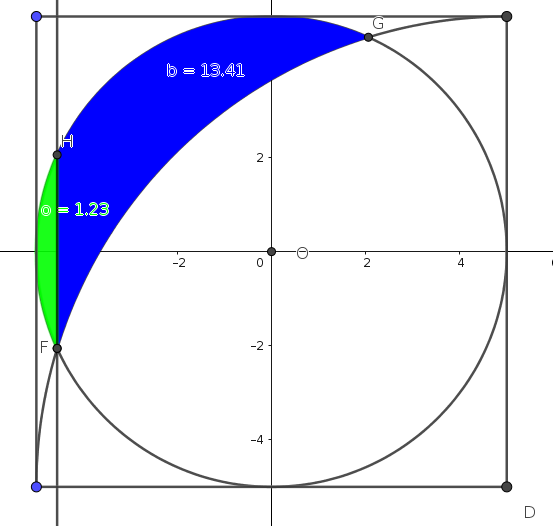
2. Bằng Máy tính cầm tay

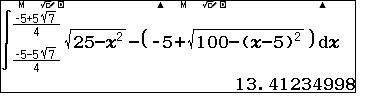
3. Bằng phép tính tích phân (dành cho học sinh lớp 12)

Chọn hệ trục tọa độ thích hợp (trục hoành và trục tung là hai đường chéo hình vuông), ta có phương trình của hai đường tròn là
$$x^2+y^2=25 \Leftrightarrow y=\pm \sqrt{25-x^2}$$
và
$$x^2+(y+5\sqrt2)^2=100\Leftrightarrow y=-5\sqrt2\pm \sqrt{100-x^2}$$

Khi đó diện tích cần tìm $$S=4\int_0^{\dfrac{5\sqrt{14}}{4}}\left[\sqrt{25-x^2}+5\sqrt2-\sqrt{100-x^2}\right]dx$$

Ta có công thức nguyên hàm
$$\int\sqrt{a^2-x^2}dx=\dfrac{x\sqrt{a^2-x^2}}{2}+\dfrac{a^2}{2}\arcsin\dfrac{x}{a}+C$$

Vậy $$S=\left[2x\sqrt{25-x^2}+50\arcsin\dfrac{x}{5}+20\sqrt2x-2x\sqrt{100-x^2}-200\arcsin\dfrac{x}{10}\right]_0^{\dfrac{5\sqrt{14}}{4}}$$

Nhận xét $\Big[2x\sqrt{25-x^2}+20\sqrt2x-2x\sqrt{100-x^2}\Big]_0^{\dfrac{5\sqrt{14}}{4}}$

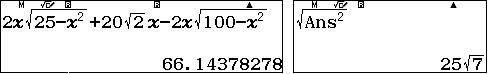
• $2\arcsin x=\arccos(1-2x^2)\Rightarrow 2\arcsin\dfrac{\sqrt{14}}{4}=\arccos\left(-\dfrac34\right)$ và $2\arcsin\dfrac{\sqrt{14}}{8}=\arccos\dfrac{9}{16}$

Tóm lại

$$S=25\sqrt7+25\arccos\left(-\dfrac34\right)-100\arccos\dfrac{9}{16}$$

Nhận xét: Tính $S$ bằng tích phân phức tạp hơn nhiều so với phép tính bằng hệ thức lượng trong tam giác. Đây chỉ là một kênh để kiểm tra đáp số.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.