Tính thể tích tứ diện trong không gian với hệ tọa độ bằng Casio fx 580vnx

Trong không gian với hệ tọa độ [latex]\large Oxyz[/latex], cho hai đường thẳng

[latex]\large d_1: \left\{\begin{matrix} x=1+t & \\ y=2-2t & \\ z=-3-t & \end{matrix}\right.[/latex] và [latex]\large d_2: \left\{\begin{matrix} x=4+3t & \\ y=3+2t & \\ z=1-t & \end{matrix}\right.[/latex]

Trên đường thẳng [latex]\large d_1[/latex] lấy hai điểm A,B thỏa AB = 3 . Trên đường thẳng [latex]\large d_2[/latex] lấy hai điểm C,D thỏa CD = 4 . Tính thể tích tứ diện V.ABCD.

A. [latex]\large V=7[/latex]         B. [latex]\large V=2\sqrt{21}[/latex]        C. [latex]\large V=\frac{4\sqrt{21}}{3}[/latex]         D. [latex]\large V=\frac{5\sqrt{21}}{6}[/latex]

Nhập ba vectơ sau đây vào máy tính:

[latex]\large \vec{u}=(1;-2;-1),\vec{v}=(3;2;-1),\overrightarrow{MN}=(3;1;4)(M(1;2;-3)\in d_1,N(3;2;-1)\in d_2)[/latex]

Ta có công thức:

[latex]\large V_{ABCD}=\frac{1}{6}AB.CD.d(AB,CD).sin(AB,CD)[/latex]

Tích có hướng [latex]\large [\vec{u},\vec{v}][/latex] 

Khoảng cách ngắn nhất giữa hai đường thẳng AB,CD là:

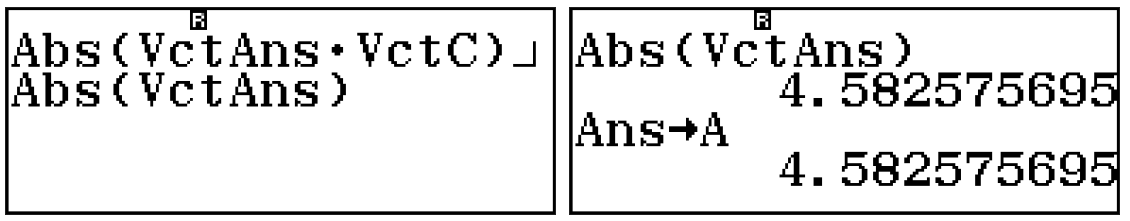
Vậy thể tích khối tứ diện ABCD là

, chọn B.

About Bitex_PTGD

Đam mê toán học. Quản trị viên Diễn Đàn Toán Casio. Mọi thắc mắc, quý thầy cô và các bạn học sinh vui lòng liên hệ vào hộp thư Inbox tại Fanpage: Diễn Đàn Toán Casio.