BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm nhanh phương trình chính tắc bằng Casio fx 580vnx
- 20/11/2018
- 683 lượt xem
Trong không gian [latex]Oxyz[/latex], cho hai đường thẳng
[latex]\large d_1: \frac{x-3}{-1}=\frac{y-3}{-2}=\frac{z+2}{1};d_2:\frac{x-5}{-3}=\frac{y+1}{2}=\frac{z-2}{1}[/latex]
và mặt phẳng [latex](P):x+2y+3z-5=0[/latex]. Đường thẳng vuông góc với [latex](P)[/latex], cắt [latex]d_1[/latex] và [latex]d_2[/latex] có phương trình là:
A. [latex]\large \frac{x-1}{1}=\frac{y+1}{2}=\frac{z}{3}[/latex]
B. [latex]\large \frac{x-2}{1}=\frac{y-3}{2}=\frac{z-1}{3}[/latex]
C. [latex]\large \frac{x-3}{1}=\frac{y-3}{2}=\frac{z+2}{3}[/latex]
D. [latex]\large \frac{x-1}{3}=\frac{y+1}{2}=\frac{z}{1}[/latex]
Nhập ba vectơ sau đây vào máy tính
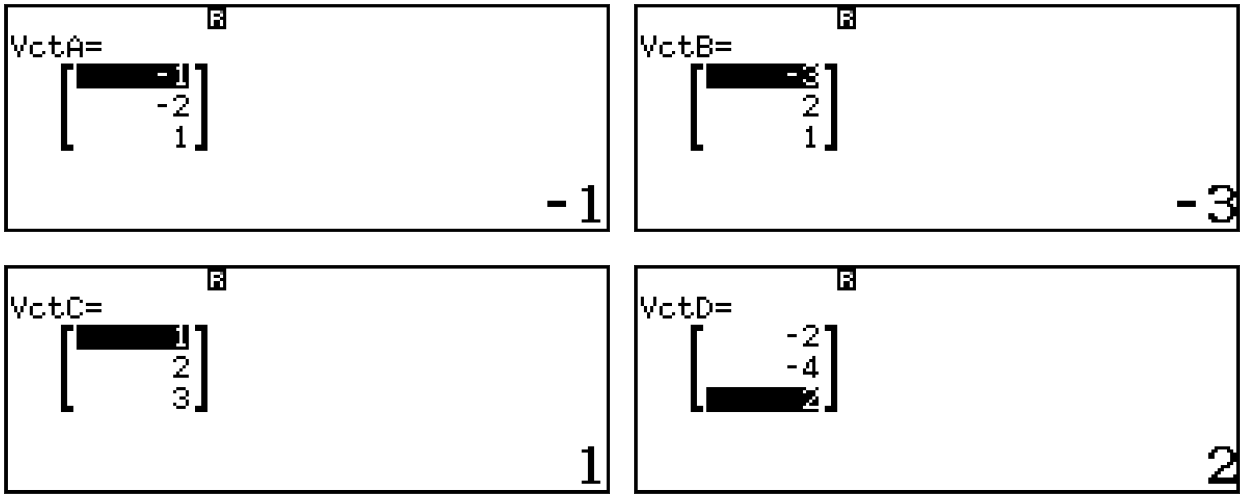
Thử phương án A: 
suy ra [latex] d_1[/latex] cắt [latex]d_A[/latex] [latex] (A_1)[/latex]
Edit vectơ VctD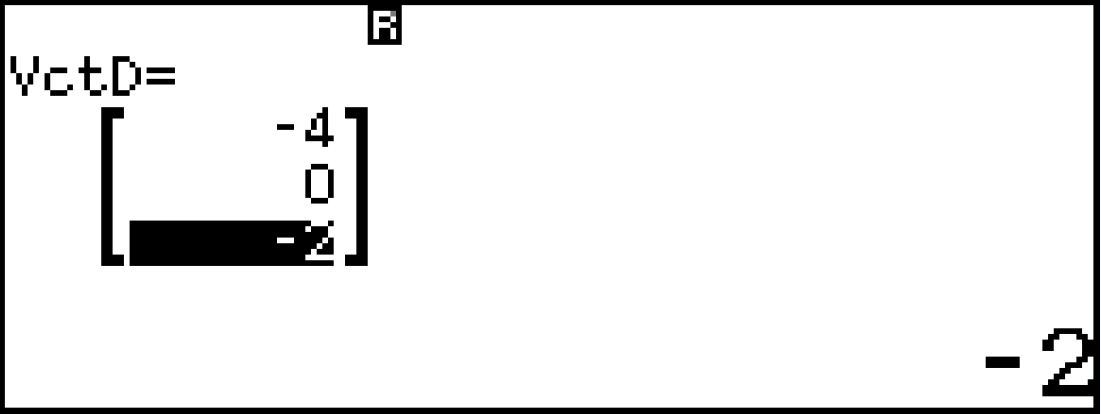 
suy ra [latex] d_2[/latex] cắt [latex] d_A[/latex]
Vậy chọn A
Lưu ý:
- Nếu phép thử [latex] (A_1)[/latex] sai thì thử tiếp phương án B.
- Nếu phải giải bài toán bằng phương pháp tự luận, ta tiến hành như sau:
Gọi [latex]\large M(3-t ,3-2t ,-2+t), N(5-3u,-1+2u,2+u)[/latex] lần lượt là giao điểm của [latex] d[/latex] với [latex] d_1[/latex] và [latex]d_2[/latex] [latex]\large \overrightarrow{MN}=(2-3u +t ,-4+2u +2t ,4+u -t)[/latex]. Theo đề bài ta có:
[latex]\large \frac{2-3u+t}{1}=\frac{-4+2u+2t}{2}=\frac{4+u-t}{3}\Leftrightarrow \left\{\begin{matrix} 4-6u +2t = -4+2u +2t & \\ -12+6u +6t = 8+2u -2t & \end{matrix}\right.[/latex]w912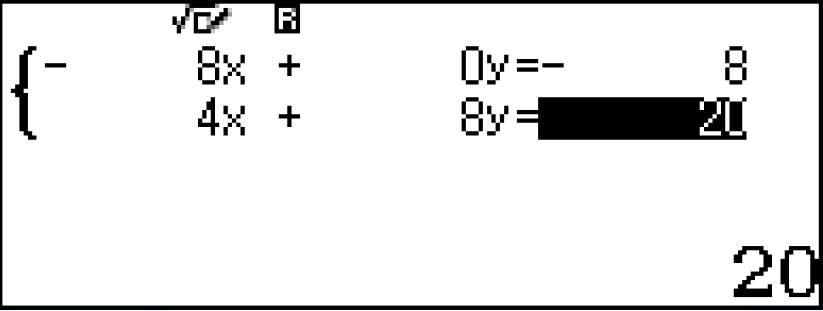 
Với [latex]\large t=2[/latex] ta có [latex]M(1,-1,0)[/latex]. Phương trình chính tắc của [latex]d[/latex] là:
[latex]\large \frac{x-1}{1}=\frac{y+1}{2}=\frac{z}{3}[/latex]About Bitex_PTGD
