BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
TÌM ĐẠO HÀM CỦA HÀM SỐ DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX
- 23/12/2021
- 3,146 lượt xem
Bài viết TÌM ĐẠO HÀM CỦA HÀM SỐ DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX sẽ trình bày 2 cách sử dụng máy tính Casio fx 580VN X để giải quyết các bài toán trắc nghiệm liên quan đến tính đạo hàm của hàm số thông qua 2 bài toán sau:
Bài toán 1. Tính đạo hàm của hàm số $y=\dfrac{x+1}{{{4}^{x}}}$
$A$. ${y}’=\dfrac{1+2\left( x+1 \right)\ln 2}{{{2}^{{{x}^{2}}}}}$
$B$. ${y}’=\dfrac{1+2\left( x+1 \right)\ln 2}{{{2}^{2x}}}$
$C$. ${y}’=\dfrac{1-2\left( x+1 \right)\ln 2}{{{2}^{2x}}}$
$D$. ${y}’=\dfrac{1-2\left( x+1 \right)\ln 2}{{{2}^{{{x}^{2}}}}}$
Hướng dẫn giải
Trong bài toán này chúng ta sẽ sử dụng chức năng tính đạo hàm tại một điểm của Casio fx- 580VN X và sau đó kiểm tra lại nghiệm
Lấy ngẫu nhiên một số bất kỳ và gán vào $X$
Tính đạo hàm của hàm số $y=\dfrac{x+1}{{{4}^{x}}}$ tại $x=X$, sau đó gán kết quả vào ô nhớ $A$
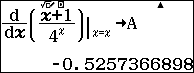
Thay và kiểm tra từng đáp án, chọn đáp án có hiệu $A-{y}’$ xấp xỉ bằng $0$
Chọn đáp án $C$
Phương pháp tự luận
${y}’={{\left( \dfrac{x+1}{{{4}^{x}}} \right)}^{\prime }}=\dfrac{{{\left( x+1 \right)}^{\prime }}{{4}^{x}}-\left( x+1 \right){{\left( {{4}^{x}} \right)}^{\prime }}}{{{\left( {{4}^{x}} \right)}^{2}}}$ $=\dfrac{{{4}^{x}}-\left( x+1 \right){{4}^{x}}\ln 4}{{{4}^{2x}}}$ $=\dfrac{1-2\left( x+1 \right)\ln 2}{{{2}^{2x}}}$
Bài toán 2. Đạo hàm của hàm số $y=\dfrac{-{{x}^{2}}+2x-3}{x-2}$ là:
$A$. ${y}’=-1-\dfrac{3}{{{\left( x-2 \right)}^{2}}}$
$B$. ${y}’=-1+\dfrac{3}{{{\left( x-2 \right)}^{2}}}$
$C$. ${y}’=1+\dfrac{3}{{{\left( x-2 \right)}^{2}}}$
$D$. ${y}’=1-\dfrac{3}{{{\left( x-2 \right)}^{2}}}$
Hướng dẫn giải
Trong bài toán này, chúng tôi sẽ sử dụng tính năng Table w8để tìm đáp án chính xác cho bài toán
Đầu tiên, chúng ta sẽ cài đặt máy tính làm việc với bảng hai hàm số qwRR12
Lấy hai số ngẫu nhiên lưu vào 2 ô nhớ $A$ và $B$
Vào phương thức TABLE w8 để kiểm tra các đáp án
Kiểm tra hai đáp án $A$ và $B$
Nhập hai hàm số $f\left( x \right)$ và $g\left( x \right)$ lần lượt ứng với hai đáp án $A$ và $B$
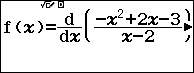
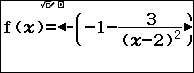
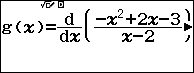
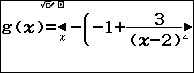
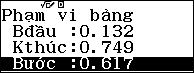
Nhập bảng giá trị $Start=B$ ; $End=A$ và $Step=A-B$ (do khi lấy ngẫu nhiên hai số $A$,$B$ thì $A>B$ )
Kết quả thu được là
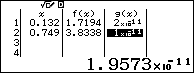
Theo định nghĩa hàm $g\left( x \right)$ ở đáp án $B$ thỏa định nghĩa ${g}’\left( x \right)=f\left( x \right)\forall x$
Chọn đáp án $B$
Cảm ơn các bạn đã theo dõi bài viết TÍNH ĐẠO HÀM CỦA HÀM SỐ DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580VN X . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580VN X , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
