SỬ DỤNG CASIO fx- 580VNX ĐỂ TÌM NHANH GTNN VÀ GTLN CỦA HÀM SỐ LƯỢNG GIÁC- PHẦN 1

Tìm GTLN và GTNN của một hàm số lượng giác là một dạng toán khó, thường khiến học sinh tốn rất nhiều thời gian và đòi hỏi khả năng kỹ thuật xử lý, biến đổi công thức lượng giác tốt khi giải bằng phương pháp tự luận truyền thống. Do đó, trong bài viết này Diễn đàn Toán Casio muốn giới thiệu đến bạn đọc cách sử dụng phương thức TABLE trên máy tính Casio fx 580VNX để tìm nhanh GTLN và GTNN của một hàm số lượng giác

Bài toán 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác:

$y=5{{\cos }^{2}}x+8\cos x\sin x-{{\sin }^{2}}x+3$

Hướng dẫn giải

Phương pháp sử dụng máy tính Casio fx 580VNX

Khảo sát hàm số $y=5{{\cos }^{2}}x+8\cos x\sin x-{{\sin }^{2}}x+3$ trên đoạn $\left[ 0;\pi  \right]$

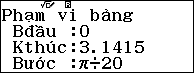
Chuyển máy tính về chế độ Radian và vào phương thức TABLE w8

Nhập vào hàm số $f\left( x \right)=5{{\cos }^{2}}x+8\cos x\sin x-{{\sin }^{2}}x+3$

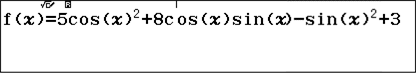
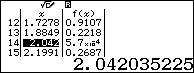
Dựa vào bảng kết quả ta dự đoán $\max \left( y \right)=10$ và $\min \left( y \right)=0$

Kiểm tra lại kết quả dự đoán

Sử dụng qr(Solve) để tìm nghiệm của phương trình $f\left( x \right)=10$

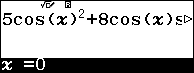
Sử dụng qr(Solve) để tìm nghiệm của phương trình $f\left( x \right)=0$

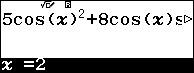
Vậy kết quả dự đoán là chính xác

Phương pháp tự luận

$y=5{{\cos }^{2}}x+8\cos x\sin x-{{\sin }^{2}}x+3$

$\Leftrightarrow y=5\dfrac{1+\cos \left( 2x \right)}{2}+4\sin 2x-\dfrac{1-\cos 2x}{2}+3$

$\Leftrightarrow y=3\cos 2x+4\sin 2x+5$

$\Leftrightarrow y-5=3\cos 2x+4\sin 2x\left( * \right)$

Điều kiện để phương trình (*) có nghiệm là

${{\left( y-5 \right)}^{2}}\le {{3}^{2}}+{{4}^{2}}$ $\Leftrightarrow {{\left( y-5 \right)}^{2}}\le 25\Leftrightarrow 0\le y\le 10$

Vậy $\max \left( y \right)=10$ và $\min \left( y \right)=0$

Dấu bằng xảy ra khi và chỉ khi $3\cos 2x+4\sin 2x=5$ hoặc $3\cos 2x+4\sin 2x=-5$

Trường hợp 1. $3\cos 2x+4\sin 2x=5$

Ta có $3\cos 2x+4\sin 2x=\sqrt{{{3}^{2}}+{{4}^{2}}}\sin \left( 2x+\alpha  \right)$ với $\cos \alpha =\dfrac{4}{5},\sin \alpha =\dfrac{3}{5}$

$\Leftrightarrow 3\cos 2x+4\sin 2x=5\sin \left( 2x+\alpha  \right)$

Như vậy$3\cos 2x+4\sin 2x=5$

$\Leftrightarrow 5\sin \left( 2x+\alpha  \right)=5$

$\Leftrightarrow \sin \left( 2x+\alpha  \right)=1$

$\Leftrightarrow 2x+\alpha =\dfrac{\pi }{2}+k2\pi $

$\Leftrightarrow x=-\dfrac{\alpha }{2}+\dfrac{\pi }{4}+k\pi $

Trường hợp 2. $3\cos 2x+4\sin 2x=-5$

Ta có$3\cos 2x+4\sin 2x=\sqrt{{{3}^{2}}+{{4}^{2}}}\sin \left( 2x+\alpha  \right)$ với $\cos \alpha =\dfrac{4}{5},\sin \alpha =\dfrac{3}{5}$

$\Leftrightarrow 3\cos 2x+4\sin 2x=5\sin \left( 2x+\alpha  \right)$

Như vậy $3\cos 2x+4\sin 2x=-5$

$\Leftrightarrow 5\sin \left( 2x+\alpha  \right)=-5$

$\Leftrightarrow \sin \left( 2x+\alpha  \right)=-1$

$\Leftrightarrow 2x+\alpha =-\dfrac{\pi }{2}+k2\pi $

$\Leftrightarrow x=-\dfrac{\alpha }{2}-\dfrac{\pi }{4}+k\pi $

Các bạn có thể tham khảo thêm một số ví dụ về bài toán Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác ở các bài viết tiếp theo

Xem tiếp SỬ DỤNG CASIO fx- 580VNX ĐỂ TÌM NHANH GTNN VÀ GTLN CỦA HÀM SỐ LƯỢNG GIÁC- PHẦN 2

Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO