BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG CASIO FX-580VNX ĐỂ KIỂM TRA NGHIỆM CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC
- 11/03/2019
- 3,164 lượt xem
Khi giải quyết các bài toán giải nghiệm của phương trình lượng giác, học sinh thường mắc phải nhiều sai sót và tốn rất nhiều thời gian. Vì vậy, việc sử dụng máy tính Casio fx 580vnx sẽ hỗ trợ rất nhiều cho các bạn học sinh trong việc tìm và kiểm tra nghiệm của phương trình lượng giác đối với cả bài toán tự luận lẫn trắc nghiệm. Dưới đây là hai ví dụ cụ thể cho việc sử dụng máy tính Casio fx 580 vnx để kiểm tra nghiệm của phương trình lượng giác.
Bài toán 1. Tìm nghiệm của phương trình lượng giác $latex \dfrac{\cos x-\sqrt{3}\operatorname{s}\text{inx}}{\operatorname{s}\text{inx}-\dfrac{1}{2}}=0$
- $latex x=\dfrac{\pi }{3}+k\pi \left( k\in \mathbb{Z} \right)$
- $latex x=\dfrac{\pi }{3}+k2\pi \left( k\in \mathbb{Z} \right)$
- $latex x=\dfrac{7\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)$
- $latex x=\dfrac{\pi }{6}+k\pi \left( k\in \mathbb{Z} \right)$
Hướng dẫn giải
Chuyển máy về chế độ Radian
Nhập biểu thức $latex \dfrac{\cos x-\sqrt{3}\operatorname{s}\text{inx}}{\operatorname{s}\text{inx}-\dfrac{1}{2}}$ vào máy:
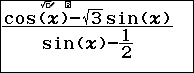
Sử dụng r để kiểm tra kết quả của biểu thức tại các giá trị :
$x=\dfrac{\pi }{3}+\pi =\dfrac{4}{3}\pi $ ; $latex x=\dfrac{\pi }{3}+2\pi =\dfrac{7\pi }{3}$ ; $latex x=\dfrac{7\pi }{6}+2\pi =\dfrac{19}{6}\pi $ và $latex x=\dfrac{\pi }{6}+2\pi =\dfrac{13}{6}\pi \\$
Bài toán 2. Tìm nghiệm của phương trình lượng giác: $latex \sqrt{3}\text{cos}\left( x+\dfrac{\pi }{2} \right)+\sin \left( x-\dfrac{\pi }{2} \right)=2\sin 2x$
Nhận xét. Khi giải quyết các bài toán phương trình lượng giác bằng phương pháp tự luận, chúng ta thường rất dễ mắc phải những sai sót trong quá trình khai triển công thức lượng giác làm ảnh hưởng đến kết quả nghiệm tìm được. Khi đó, máy tính cầm tay sẽ hỗ trợ việc kiểm tra việc đúng, sai của nghiệm tìm được
Hướng dẫn giải
$\sqrt{3}\text{cos}\left( x+\dfrac{\pi }{2} \right)+\sin \left( x-\dfrac{\pi }{2} \right)=2\sin 2x\\$
$\Leftrightarrow -\sqrt{3}\operatorname{sinx}-\operatorname{cosx}=2\sin 2x\\$
$\Leftrightarrow \dfrac{\sqrt{3}}{2}\operatorname{s}\text{inx+}\dfrac{1}{2}\cos x=-\sin 2x$ (1)
Nhận thấy
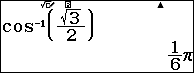
Nên ta có:
$\left( 1 \right)\Leftrightarrow \cos \left( \dfrac{\pi }{6}\right)\operatorname{s}\text{inx}+\sin\left( \dfrac{\pi }{6} \right)\cos x=\sin \left( -2x\right)\\$
$\Leftrightarrow \sin \left( \dfrac{\pi }{6}+x \right)=\sin \left( -2x \right)\\$
$\Leftrightarrow \left[ \begin{align} & \dfrac{\pi }{6}+x=-2x+k2\pi \left( k\in \mathbb{Z}\right) \\ & \dfrac{\pi }{6}+x=\pi +2x+k2\pi \left( k\in \mathbb{Z} \right) \\\end{align} \right.\\$
$\Leftrightarrow \left[ \begin{align} & x=-\dfrac{\pi }{18}+\dfrac{k2\pi }{3}\left( k\in \mathbb{Z} \right) \\ & x=-\dfrac{5\pi }{6}-k2\pi \left( k\in \mathbb{Z} \right) \\ \end{align} \right.\\$
Vậy phương trình đã cho có 2 họ nghiệm: $latex x=-\dfrac{\pi }{18}+\dfrac{k2\pi }{3}$ và $latex x=-\dfrac{5\pi }{6}-k2\pi $$latex \left( k\in \mathbb{Z} \right)$
Sử dụng máy tính Casio fx 580vnx kiểm tra các nghiệm trên
Chuyển máy tính về chế độ Radian
Nhập vào máy biểu thức: $latex \sqrt{3}\text{cos}\left( x+\dfrac{\pi }{2} \right)+\sin \left( x-\dfrac{\pi }{2} \right)-2\sin 2x$
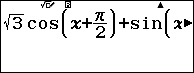
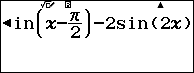
Sử dụng r để kiểm tra kết quả của biểu thức tại các giá trị
Chọn $latex k=1$ :
Ứng với họ nghiệm $latex x=-\dfrac{\pi }{18}+\dfrac{k2\pi }{3}$ ta thử $latex x=\dfrac{11}{18}\pi $
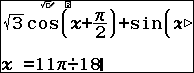
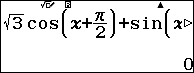
Ứng với họ nghiệm $latex x=-\dfrac{5\pi }{6}-k2\pi $ ta thử $latex x=-\dfrac{17}{6}\pi $
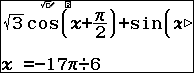
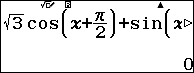
Dựa vào kết quả kiểm tra ta thấy 2 họ nghiệm tìm được là nghiệm của phương trình lượng giác đã cho.
About Ngọc Hiền Bitex
