BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
MỘT SỐ CÔNG THỨC HÌNH HỌC THƯỜNG SỬ DỤNG TRONG KỲ THI HSG TOÁN CASIO
- 27/07/2022
- 1,663 lượt xem
Trong những kì thi học sinh giỏi giải toán trên máy tính cầm tay, các câu hỏi về hình học thường gây nhiều khó khăn cho thí sinh, một phần là do các bạn không nhớ và vận dụng hết được các công thức. Do đó, trong bài viết này Diễn đàn Toán Casio sẽ tóm tắt một số công thức tính toán hình học thường dùng trong cacs kì thi HSG Toán Casio
Trong những kì thi học sinh giỏi giải toán trên máy tính cầm tay, các câu hỏi về hình học thường gây nhiều khó khăn cho thí sinh, một phần là do các bạn không nhớ và vận dụng hết được các công thức. Do đó, trong bài viết này Diễn đàn Toán Casio sẽ tóm tắt một số công thức tính toán hình học thường dùng trong cacs kì thi HSG Toán Casio
1) Định lý Pitago $a^2=b^2+c^2$
2) Định lý Ceva: AM, BN, CP đồng quy
$\dfrac{\overline{MB}}{\overline{NC}}.\dfrac{\overline{NC}}{\overline{NA}}.\dfrac{\overline{PA}}{\overline{PB}}=-1$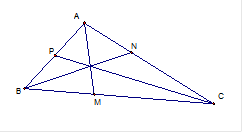 
3)Định lý Mencleit: M, N, P thẳng hàng : $\dfrac{\overline{MB}}{\overline{NC}}.\dfrac{\overline{NC}}{\overline{NA}}.\dfrac{\overline{PA}}{\overline{PB}}=1$
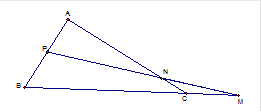
4) Công thức lượng giác:
a) Tam giác vuông:
$BA^2=BH.BC$
$BC^2=AC^2+AB^2$
$AH^2=HB.HC$
$\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{C}^{2}}}$
b) Tam giác thường:
– Trung tuyến: $A{{M}^{2}}=\dfrac{1}{2}(A{{B}^{2}}+A{{C}^{2}})-\dfrac{B{{C}^{2}}}{4}$
– Định lý hàm số Sin: $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
– Định lý hàm số Cosin: $a^2=b^2+c^2-2bccosA$
– Diện tích: S =$\dfrac{1}{2}a{{h}_{a}}=\dfrac{1}{2}ab\sin C=pr=\dfrac{abc}{4R}=\sqrt{p(p-a)(p-b)(p-c)}$
– Đường phân giác: ${{l}_{a}}=\dfrac{2bc\cos \dfrac{A}{2}}{b+c}$
c) Tam giác đều: Diện tích, chiều cao: S= $\dfrac{{{a}^{2}}\sqrt{3}}{4};{{h}_{a}}=\dfrac{a\sqrt{3}}{2}$
d) Diện tích hình quạt: $S=\dfrac{\pi {{R}^{2}}\alpha }{{{360}^{0}}}$
5) Diện tích, thể tích:
– Hình chóp: $V=\dfrac{1}{3}Bh$
– Hình nón: $V=\dfrac{1}{3}\pi {{R}^{2}}h;{{S}_{xq}}=\pi Rl$
– Hình chóp cụt: $V=\dfrac{1}{3}(B+\sqrt{BB’}+B’)h$
– Hình nón cụt: $V=\dfrac{1}{3}\pi ({{R}^{2}}+RR’+R{{‘}^{2}})h;{{S}_{xq}}=\pi (R+R’)l$
– Hình cầu: $V=\dfrac{4}{3}\pi {{R}^{3}};{{S}_{xq}}=4\pi {{R}^{2}}$
– Hình trụ: $V=\pi {{R}^{2}}h;{{S}_{xq}}=2\pi Rh$
– Hình chỏm cầu: $V=\pi {{h}^{2}}(R-\dfrac{h}{3});S=2\pi Rh$
About Ngọc Hiền Bitex
