GIẢI BÀI TOÁN TRẢ NỢ DẦN với MÁY TÍNH CASIO FX 580VNX
- 07/02/2020
- 673 lượt xem
Bài toán Trả nợ dần (Amortization) là một phần của bộ môn Toán tài chính. Trong chương trình hiện hành nó thể hiện ở bài toán mua hàng trả góp. Trong Chương trình giáo dục phổ thông mới, Toán tài chính là một chuyên đề tự chọn của lớp 12. Các học sinh có nguyện vọng theo học ĐH Kinh tế (ngành Tài chính kế toán), Đại học ngân hàng v.v. .. sẽ có khuynh hướng chọn chuyên đề này.
Để giúp các thầy cô làm quen với môn học này, đồng thời cũng giúp cho học sinh 12 giải được bài toán thực tế có liên quan của kỳ thi THPT QG năm 2020, chúng tôi viết loạt bài này và sau đó thực hiện một series các video để hướng dẫn trực quan.
1. Một số định nghĩa và công thức:
Gọi $P$ là một khoản vay ngân hàng (hoặc một tổ chức tín dụng) để trả hàng tháng vào cuối mỗi tháng, mỗi tháng trả một số tiền như nhau là $R$ với kỳ hạn $n$ tháng và lãi suất $i$/tháng.
$R$ còn gọi là tô (Thời phong kiến nông dân có hình thức phát canh thu tô cũng theo mô hình này).
tô gồm có hai phần: Lãi (của ngân hàng) và tiền nạp vào nợ gốc (để làm giảm nợ gốc). Nếu bạn đã từng vay tiền của ngân hàng (theo hình thức tín chấp), bạn sẽ nhận được một phụ lục hợp đồng, trong đó ngân hàng liệt kê từng tháng số tiền bạn phải đóng (tiền nạp vào nợ gốc) và lãi của ngân hàng.
Dưới đây chúng tôi giới thiệu công thức tính hai khoản tiền nói trên.
$R$ (tô) là nghiệm của phương trình:
$$P(1+i)^n=\dfrac{R}{i}((1+i)^n-1)$$
Số dư nợ (số tiền còn nợ lại) sau khi thanh toán đến tháng thứ $k$ là:
$$P_k=P(1+i)^k-\dfrac{R}{i}((1+i)^k-1)$$
Lãi bằng lãi suất nhân cho dư nợ của kỳ thanh toán trước.
Tiền nạp vào nợ gốc bằng tô trừ đi lãi.
2. Bài tập áp dụng
Bài 1: Một khoản vay $\$5000$ được trả dần hàng tháng vào cuối mỗi tháng trong hai năm với lãi kép 7%/năm. Tìm số dư nợ sau 8 tháng.
Giải: Tô, tức là số tiền hàng tháng phải trả cho khoản vay, là nghiệm của phương trình:
$$5000\left(1+\dfrac{7\%}{12}\right)^{24}=\dfrac{R}{\dfrac{7\%}{12}}\left(\left(1+\dfrac{7\%}{12}\right)^{24}-1\right)$$
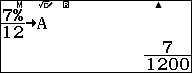
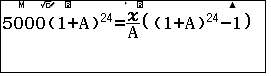

Khi tính được $R$, ta tính được số dư nợ sau 8 tháng là
 lưu vào B.
lưu vào B.
(lấy vốn và lãi gộp sau 8 tháng trừ đi tổng số tiền trả nợ dần trong 8 tháng đó)
Vậy số dư nợ sau 8 tháng là $\$3410.26$ (làm tròn đến hai sổ lẻ thập phân).
Bài 2: Một khoản vay $\$5,000$ được trả dần hàng tháng vào cuối mỗi tháng trong hai năm với lãi kép 7%/năm. Tìm tiền lãi và tiền nạp vào nợ gốc (để làm giảm nợ gốc) của lần thanh toán thứ 9.
Giải: Tiền lãi của lần thanh toán thứ 9 bằng lãi suất (A) nhân với dư nợ sau 8 tháng (B)

tiền nạp vào nợ gốc (để làm giảm nợ gốc) của lần thanh toán thứ 9 là

Bài 3: Một khoản $\$35,000$ được vay để mua một chiếc xe hơi. Khoản vay này sẽ trả dần hàng tháng vào cuối mỗi tháng trong ba năm với lãi kép 3%/năm. Tìm tổng số tiền lãi trong 12 lần thanh toán của năm thứ hai .
Giải:
Tô được xác định là nghiệm của phương trình:
$$35000\left(1+\dfrac{3\%}{12}\right)^{36}=\dfrac{R}{\dfrac{3\%}{12}}\left(\left(1+\dfrac{3\%}{12}\right)^{36}-1\right)$$

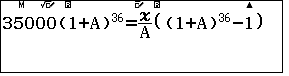
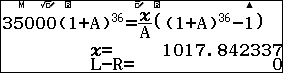

Để cho gọn ta lưu $1+A$ vào $z$ 
Lãi trong lần thanh toán thứ $x$ là $$A(Fz^x-\dfrac{B}{A}(z^x-1))$$
Vậy tổng số tiền lãi trong 12 lần thanh toán của năm thứ hai là:
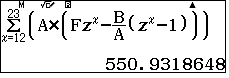
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay