Dành cho các bạn yêu thích máy tính Casio 580 VNX
- 06/05/2020
- 655 lượt xem
Sở dĩ chúng tôi đặt tiêu đề như vậy là vì có nhiều tính năng hoạt động tốt trên máy tính nhưng đòi hỏi phải được giải thích chi tiết và thao tác không đơn giản. Tuy nhiên với tư cách là một học thuật, bài viết này hữu ích cho giáo viên toán và cho học sinh giỏi.
Bài toán: Trong không gian $Oxyz$ cho 4 diểm không đồng phẳng $A, B, C, D$. Tính khoảng cách từ điểm $D$ đến mặt phẳng $(ABC)$.
Trước hết chúng tôi hướng dẫn thao tác trên máy tính. Sau đó chúng tôi có một bài riêng thuần túy toán học để giải thích sự kiện.
Thao tác trên máy tính
- Nhập ba trận cấp 3 sau vào máy tính
$$A=\left(\begin{array}{ccc}
x_A&y_A&1\\
x_B&y_B&1\\
x_C&y_C&1
\end{array}\right), B=\left(\begin{array}{ccc}
y_A&z_A&1\\
y_B&z_B&1\\
y_C&z_C&1
\end{array}\right), C=\left(\begin{array}{ccc}
x_A&z_A&1\\
x_B&z_B&1\\
x_C&z_C&1
\end{array}\right)$$Chú ý ma trận $A$ chỉ khác ma trận $C$ ở cột 2 nên dễ thực hiện, tương tự ma trận $C$ chỉ khác ma trận $B$ chỉ khác nhau ở cột thứ nhất.
- Nhập ma trận cấp 4 sau đây vào máy tính
$$D=\left(\begin{array}{cccc}
x_A&y_A&z_A&1\\
x_B&y_B&z_B&1\\
x_C&y_C&z_C&1\\
x_D&y_D&z_D&1
\end{array}\right)$$ - Tính định thức các ma trận $A, B, C, D$ lần lượt lưu vào A, B, C, D.
- $d(D, (ABC))=\dfrac{|D|}{\sqrt{A^2+B^2+C^2}}$
Áp dụng: Cho hình chóp $S . ABCD$ có đáy là hình vuông cạnh $a$ , mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ $A$ đến mặt phẳng $( SBD )$ bằng$A. \dfrac{\sqrt{21}a}{14}\qquad B. \dfrac{\sqrt{21}a}{7}\qquad C. \dfrac{\sqrt{2}a}{2}\qquad D.\dfrac{\sqrt{21}a}{28}$
Giải
Chọn hệ trục tọa độ thích hợp, ta có:
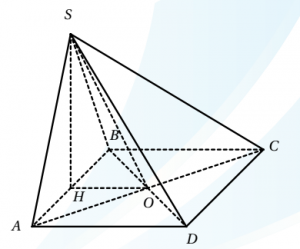
$$S\left(0;0;\dfrac{\sqrt3}{2}\right) ; B\left(-\dfrac12;0;0\right) ; D\left(\dfrac12;1;0\right) ; A\left(\dfrac12;0;0\right)$$
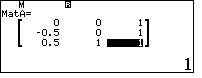

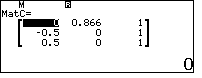
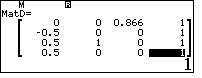


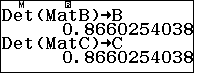



Đón đọc bài tiếp theo:
Cơ sở toán học nào dẫn đến thao tác trên máy tính Casio fx-580 VNX như trên.
PS. Nếu vẽ hình cẩn thận ta có thể giải bài toán này một cách khác như sau:
$d(A,(SBD)=d(A,(SBO))$
Phương trình mặt phẳng $(SBO)$ là $\dfrac{x}{-\dfrac12}+\dfrac{y}{\dfrac12}+\dfrac{z}{\dfrac{\sqrt3}{2}}=1$
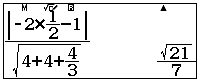
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay