Cách tìm ra nghiệm đơn và nghiệm kép trong phương trình bậc 3
- 11/08/2022
- 20,334 lượt xem
Ví dụ minh hoạ: Tìm số điểm cực tiểu của hàm số $f(x)=\frac{x^4}{4}-\frac{4}{3}x^3+\frac{5}{2}x^2-2x+4$
A. 3 B. 2 C. 1. D. 0.
Lời giải
-Đạo hàm $f'(x)$ tìm nghiệm của $f'(x)=0$.
$f'(x)=x^{3}-4x^{2}+5x-2=0$

Dễ thấy phương trình bậc 3 phải có 3 nghiệm nhưng trong phương trình này chỉ có 2 nghiệm, chứng tỏ trong 2 nghiệm này có 1 nghiệm kép và 1 nghiệm đơn.
Các bước để xác định nghiệm kép:
Bước 1: tách hàm bậc 3 theo 2 nghiệm mà máy tính bấm được. Khi tách sẽ xảy ra 2 trường hợp.
1. $f'(x)=(x-1)^{2}(x-2)$ khi $x=1$ là nghiệm kép.
2. $f'(x)=(x-1)(x-2)^{2}$ khi $x=2$ là nghiệm kép.
Bước 2: Lấy hệ số không chưa biến nhân lại với nhau nếu ra $-2$ (hệ số không chưa biến của $f'(x)$) thì đó là $f'(x)$ cần tìm
1.$f'(x)=(x^{2}-2x+1)(x-2)\Rightarrow$ phần hệ số $1.(-2)=-2$ thoả mãn.
2.$f'(x)=(x-1)(x_{2}-4x+4)\Rightarrow $ phần hệ số $(-1).4=-4$ không thoả mãn.
Vậy $f'(x)=(x^{2}-2x+1)(x-2)=0$ có nghiệm đơn $x=2$ và nghiệm kép $x=1$
Kiểm tra xem hàm số $f(x)$ có đạt cực tiểu tại $x=2$ không?
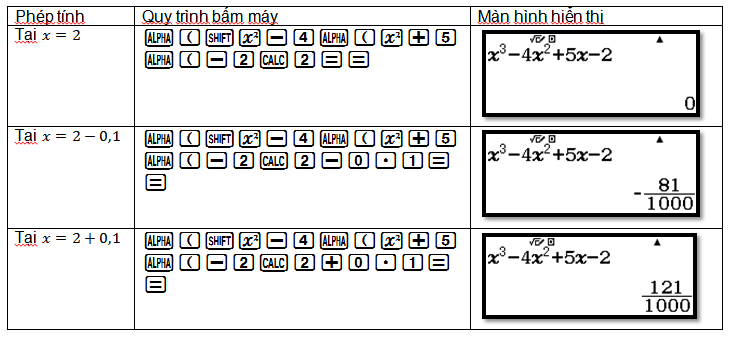
$f'(x)$ đổi dấu từ $(-)$ sang $(+)$ $\Rightarrow x=2$ là cực tiểu của hàm số $f(x)$
Chọn C.
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay