BÀI GIẢI MINIGAME 1 (GIẢI TÍCH)

Câu 1:  Cho $f$ là hàm số liên tục trên đoạn $\left[0;\dfrac{\pi}{4}\right ]$ và thoả đẳng thức:

$2f(x)+3f\left(\dfrac{\pi}{4}-x\right)=\sqrt{\tan x}$.

Đặt $\displaystyle I=\int_0^\dfrac{\pi}{4}f(x)dx$.

Hỏi $I$ gần đúng với giá trị nào sau đây:

A. $0,0975$              B. $1,0975$                  C. $0,4875$               D.$1,4875$

Câu 2: Câu hỏi phụ. Biết $I$ được viết dưới dạng:

$I=\dfrac{\sqrt{2}}{20}\left[a\pi +b\ln(3+2\sqrt{2})\right]$

với $a$ và $b$ là hai số nguyên.

A. $a+b=0$         B. $a+b=1$          C. $a+b=-1$                    D. $a-b=0$

Bài giải:

Câu 1: Cho $f$ là hàm số liên tục trên đoạn $\left[a;b\right]$, ta có công thức

$$\int_a^bf(x)dx=\int_a^bf(a+b-x)dx$$

Chứng minh bằng công thức đổi biến số, đặt $t=a+b-x$.

Áp dụng công thức, lấy tích phân hai vế của đẳng thức

$$2f(x)+3f\left(\dfrac{\pi}{4}-x\right)=\sqrt{\tan x}$$

ta có:

$$5I=\int_0^{\pi/4}\sqrt{\tan x}dx \Rightarrow I= \dfrac{1}{5}\int_0^{\pi/4}\sqrt{\tan x}dx$$

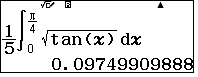
chọn A.

Câu hỏi phụ.

• Tính  $I$ trên máy tính lưu vào F
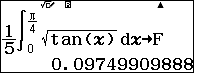
• Đặt $a=x$ thử phương án A với $a+b=0\Rightarrow b=-x$ thay vào phương trình

$I=\dfrac{\sqrt{2}}{20}\left[a\pi +b\ln(3+2\sqrt{2})\right]$

• Bấm SHIFT SOLVE, khi máy hỏi F bấm mũi tên xuống, khi máy tính hỏi X, nhập X=0 rồi nhấn =
  
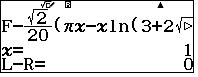
• Vậy với $a=1, b=-1$ ycbt được thỏa. Vậy ta chọn A.

Bài giải tự luận tính tích phân $K=\displaystyle \int_0^{\pi/4}\sqrt{\tan x}dx$.

Đặt $t=\sqrt{\tan x}\Rightarrow dx=\dfrac{2dt}{1+t^4}$.

Khi đó: $K=\displaystyle \int_0^{\pi/4}\sqrt{\tan x}dx=\int_0^1\dfrac{2t^2dt}{1+t^4}$.

Bằng phương pháp hệ số bất định ta phân tích được:

$$\dfrac{2t^2}{1+t^4}=\dfrac{\sqrt2}{2}\left[\dfrac{t}{t^2-t\sqrt2+1}-\dfrac{t}{t^2+t\sqrt2+1}\right]$$

Biến đổi

$$\dfrac{2t^2}{1+t^4}=\dfrac{\sqrt2}{4}\left[\dfrac{2t-\sqrt2+\sqrt2}{t^2-t\sqrt2+1}-\dfrac{2t+\sqrt2-\sqrt2}{t^2+t\sqrt2+1}\right]$$

Áp dụng công thức: $\displaystyle \int\dfrac{dx}{ax^2+bx+c}=\dfrac{2}{\sqrt{-\Delta}}\left[\arctan\dfrac{2ax+b}{\sqrt{-\Delta}}\right]+C$

với $\Delta =b^2-4ac <0$, ta có:

$$K=\int_0^1\dfrac{2t^2dt}{1+t^4}=\dfrac{\sqrt2}{4}\left[\ln\dfrac{t^2-t\sqrt2+1}{t^2+t\sqrt2+1}+2\arctan(t\sqrt2-1)+2\arctan(t\sqrt2+1)\right]_0^1$$

$$K=\int_0^1\dfrac{2t^2dt}{1+t^4}=\dfrac{\sqrt2}{4}\left[\pi -\ln(3+2\sqrt2)\right]$$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.