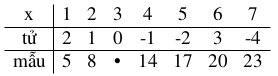BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng tính năng lập bảng
- 19/11/2021
- 301 lượt xem
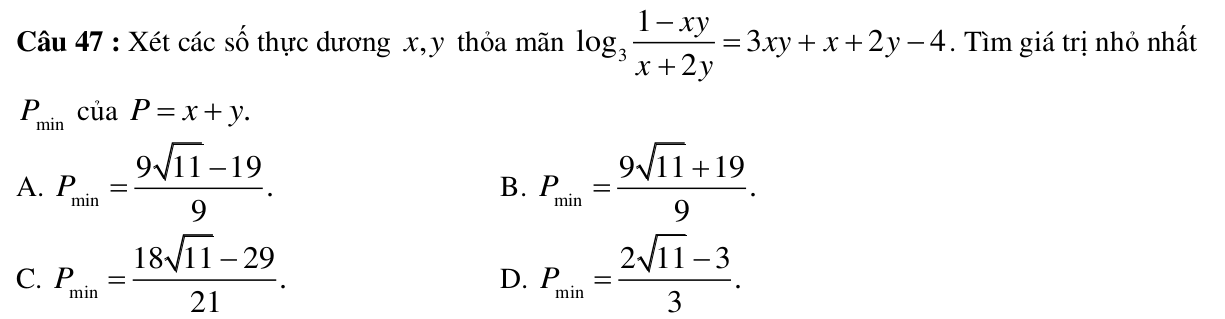
Lời giải tự luận cho bài toán đã được nhiều thầy cô giới thiệu ngay khi câu trắc nghiệm này được công bố. Lời giải đó phụ thuộc vào khả năng biến dổi của học sinh để đưa đẳng thức đã cho về dạng $$f(A)=f(B)$$với $f$ là hàm số đơn diệu để dẫn đến đẳng thức $A=B$ và từ đó tính được $y$ theo $x$.
Cũng với ý tưởng đó, chúng tôi giới thiệu thêm việc sử dụng tính năng lập bảng để tính $y$ theo $x$, xem như một cách khác để giải quyết vấn đề.
Trước hết ta viết lên màn hình phương trình đã cho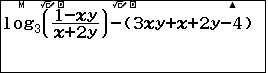 
Sau đó lần lượt cho $x=1,2,3,4,5,6,7$ và giải phương trình tìm $y$ tương ứng.
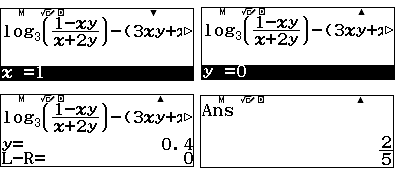
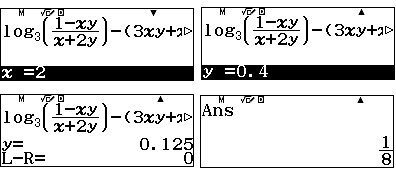
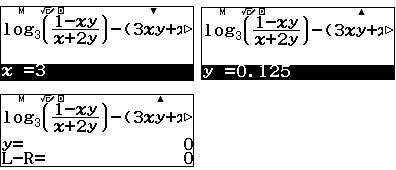
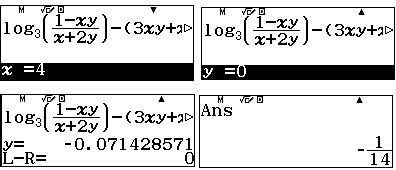
| Ta lập bảng giá trị
Ta thấy mối quan hệ giữa $x$ và tử là “tuyến tính” nghĩa là các điểm có hoành độ $x$ và tung độ là “tử” nằm trên đường thẳng $y=3-x$. Tương tự mối quan hệ giữa $x$ và mẫu là “tuyến tính” nghĩa là các điểm có hoành độ $x$ và tung độ là “mẫu” nằm trên đường thẳng $y=3x+2$ (chỉ cần nhẫm phương trình đường thẳng đi qua hai điểm đầu tiên).
Tóm lại ta dự đoán $y=\dfrac{3-x}{3x+2}$. Câu trắc nghiệm không cần chứng minh dự đoán này. Vậy ta có hàm số $$P=x+\dfrac{3-x}{3x+2}, 0<x<3$$ Ta có nhận xét rằng đồ thị hàm số là một hyperbol xiên góc, với điều kiện $0<x<3$ phần đồ thị thuộc nhánh phải của hyperbol và GTNN chính là giá trị cực tiểu. Ta tìm giá trị cực tiểu trên máy tính Casio fx-580VN X như sau:
|
About TS. Nguyễn Thái Sơn
