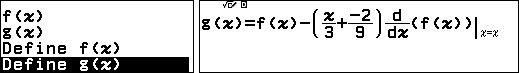SỬ DỤNG TÍNH NĂNG FUNCTION VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM CỰC TRỊ

Trước hết ta có nhận xét nếu lấy $y=ax^3+bx^2+cx+d$ chia cho đạo hàm $y’=3ax^2+2bx+c$ thì thương là $\dfrac{x}{3}+\dfrac{b}{9a}$ do đó dư sẽ là $$g(x)=y-y’\left(\dfrac{x}{3}+\dfrac{b}{9a} \right)$$

Khi đó $y=g(x)$ sẽ là đường thẳng đi qua hai điểm cực trị. Muốn tìm hai hệ số của đường thẳng này ta tính $g(0)$ và $g(1)-g(0)$.

Bấm vào phím FUNCTION rồi chọn   Lại bấm vào phím FUNCTION rồi chọn   Bấm phím HOME để trở ra, vào màn hình tính toán thhông thường và thực hiện phép tính Vậy phương trình đường thẳng đi qua hai điểm cực trị là: $y=-\dfrac{2}{9}x+\dfrac{20}{9}$.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.