SỬ DỤNG MÁY TÍNH CASIO FX-580VN X TRONG CHUYÊN ĐỀ TÍNH THỂ TÍCH TRONG HÌNH HỌC KHÔNG GIAN

22/04/2021
1,242 lượt xem
Toanbitexdtgd

Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = $a\sqrt{3}$ , SA vuông góc với mặt phẳng đáy. Biết góc giữa SC và (ABC) bằng $60^{\circ}$ . Tinh thể tích khối chóp S.ABC theo a.

Hướng dẫn:

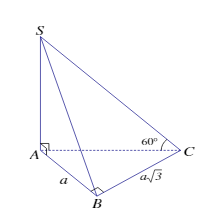
Ta có:

$\Delta ABC$ vuông tại B $\Rightarrow S_{ABC}=\frac{1}{2}AB.BC=\frac{a^{2}\sqrt{3}}{2}$

$SA \bot (ABC)$ nên AC là hình chiếu của SC lên (ABC)

Do đó góc giữa SC và (ABC) là $\widehat{SCA}=60^{\circ}$

$\Delta ABC$ vuông tại B $\Rightarrow AC=\sqrt{AB^{2}+BC^{2}}=2a$

$\Delta SAC$ vuông tại A $\Rightarrow SA= AC.tan60^{\circ}=2a\sqrt{3}$

Thể tích khối chóp S.ABC là $V_{S.ABC}=\frac{1}{3}SA.S_{ABC}=a^{3}$

Sủ dụng máy tính:

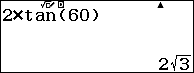
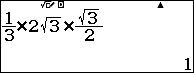
Bài 2: Cho hinh chóp S.ABCD có đáy là hình vuông canh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính theo a khỏang cách từ điểm A đến măt phẳng (SCD).

Hướng dẫn:

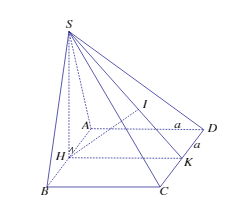
Gọi H là trung điểm AB $\Rightarrow SH \bot AB$ ( do $\Delta SAB$ đều)

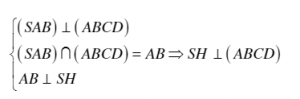
Tam giác SAB đều nên SH = $\frac{a\sqrt{3}}{2}$

Ta có:

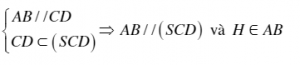
d(A, (SCD)) = d( H, (SCD))

Gọi K là trung điểm CD và I là hình chiếu vuông góc của H lên SK.

Khi đó:

Và :

Do đó: d( A, (SCD))=HI = $\frac{SH.HK}{\sqrt{SH^{2}+HK^{2}}}=\frac{a\sqrt{21}}{7}$

Sử dụng máy tính:

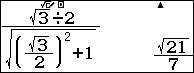
Bài 3: Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA =OB= OC=a. Gọi I là trung điểm BC. Khoảng cách giữa và AI và OC bằng bao nhiêu?

Hướng dẫn:

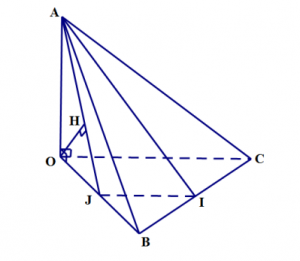
Gọi J là trung điểm OB $\Rightarrow$ IJ // OC $\Rightarrow$ OC // (AIJ)

Suy ra: d( AI,OC) = d (OC,(AIJ)) =d (O, (ẠIJ))

Kẻ OH vuông góc AJ tại H.

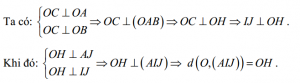
Vì $\Delta$ AOJ vuông tại O, có OH là đường cao.

Suy ra OH= $\frac{OA.OJ}{\sqrt{OA^{2}+OJ^{2}}}=\frac{a.\frac{a}{2}}{\sqrt{a^{2}+(\frac{a}{2})^{2}}}=\frac{a}{\sqrt{5}}$

Vậy d( AI, OC) = OH = $\frac{a\sqrt{5}}{5}$ .

Sử dụng máy tính:

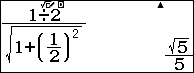
Bài 4: Cho hình trụ có hai đáy là hai hình tròn (O) và (O’) , chiều cao bằng 2R và bán kính đáy bằng R . Một mặt phẳng ( $\alpha$ ) đi qua trung điểm của OO’ và tạo với OO’ một góc bằng $30^{\circ}$ , ( $\alpha$ ) cắt hình tròn đáy theo một đoạn thẳng có độ dài l. Tính l theo R .

Hướng dẫn:

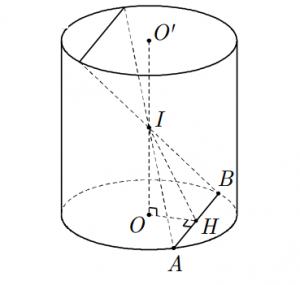
Giả sử ( $\alpha$ ) cắt hình tròn (O,R) theo dây cung AB.

Gọi I là trung điểm OO’, H là trung điểm dây cung AB.

Ta có AB $\bot$ (OIH) từ đó suy ra được $(\widehat{OO,(\alpha )})=\widehat{OIH}\Rightarrow \widehat{OIH} = 30^{\circ}$

Ta có: OH=OI.tan $\widehat{OIH}=\frac{R}{\sqrt{3}}$

Suy ra AB= $2\sqrt{R^{2}-\frac{R^{2}}{3}}=\frac{2R\sqrt{6}}{3}$

Sử dụng máy tính:

Bài 5: Cho hình nón đỉnh S, có chiều cao h=a và bán kính đáy r=2a. Mặt phẳng (P) đi qua S, cắt đường tròn đáy tại A và B sao cho AB= $2\sqrt{3}a$ . Tính khoảng cách d từ tâm của đường tròn đáy đến mặt (P).

Hướng dẫn:

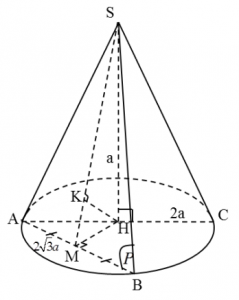
Gọi H là tâm của mặt đáy ( ABC), M là trung điểm của AB, K là hình chiếu của H lên SM, mặt (P) cắt hình nón theo thiết diện là $\Delta$ SAB.

Xét tam giác AMH vuông tại M có:

$MH=\sqrt{AH^{2}-AM^{2}}=\sqrt{AH^{2}-(\frac{AB}{2})^{2}}=\sqrt{\left ( 2a \right )^{2}-(\sqrt{3}a)^{2}}=a$

Vì K là hình chiếu của H lên SM nên d(H,(P))=HK

Xét tam giác SHM vuông tại H có:

$\frac{1}{HK^{2}}=\frac{1}{SH^{2}}+\frac{1}{MH^{2}}=\frac{1}{a^{2}}+\frac{1}{a^{2}}$

$\Rightarrow HK=\frac{\sqrt{2}}{2}a$ .

Sử dụng máy tính:

Từ khóa:

#casio thể tích trong hhkg

Chia sẻ

H	B	T	N	S	B	C
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay

SỬ DỤNG MÁY TÍNH CASIO FX-580VN X TRONG CHUYÊN ĐỀ TÍNH THỂ TÍCH TRONG HÌNH HỌC KHÔNG GIAN

About Bitex Khánh Vũ

Bài viết liên quan

Bài Viết Tương Tự

Sử dụng PPTĐ trong không gian $Oxyz$

BẢN TIN

ĐĂNG KÝ NHẬN BẢN TIN