Sử dụng máy tính cầm tay giải bài toán VDC về phương trình mũ

(mã đề 102)

Phương trình  đã cho có thể được  viết $$(4x-4-y)e^x=-2yx^2+y^2x-3y \quad (1)$$

Đặt $f(x)=(4x-4-y)e^x$ ta thấy hàm số đạt cực tiểu tại $x=\dfrac{y}{4}$.

Nếu $y<4$ hàm số đạt giá trị nhỏ nhất trên $[1;5]$    là $\min \{f(1), f(5)\}= f(1)=-ye$.

$g(x)=-2yx^2+y^2x-3y$, ta thấy hàm số đạt cực đại tại $x=\dfrac{y}{4}$.

Nếu $y<4$ hàm số đạt giá trị lớn nhất trên $[1;5]$    là $\max \{g(1),g(5)\}=g(1)=y^2-5y$.

Ta thấy $f(x) > -ye , g(x)<y^2-5y\ \forall \ x \in (1;5)$. Xét bất phương trình  $-ye>y^2-5y$

$\Leftrightarrow 0<y<2,28$. Vậy nếu $y=1 \vee y=2$ thì $f(x)>g(x)\ \forall x \in (1;5)$, nghĩa là phương trình  (1) không có nghiệm trên khoảng $(1;5)$.

1. 1. 1. Viết lên màn hình phương trình 
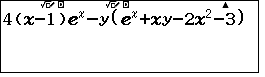
   2. 2. Bấm SHIFT SOLVE nhập $x$, nhập $y$ trở lại màn hình $x$, nhấn = 
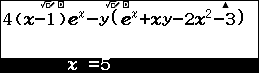
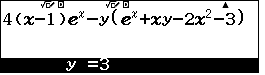
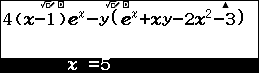
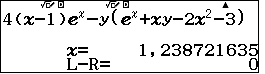
   3. 3. Lặp lại với
      $y=4$ , $y=5$  $y=6$
      $y=7$ $y=8$ $y=9$ 
      $y=10$   $y=11$ $y=12$
      $y=13$ $y=14$

1. $\bullet\ $ Mỗi lần bấm SHIFT SOLVE mất khoảng 5 giây nên sau 13 lần bấm ta mất khoảng 65 giây thì kết thúc. Về phương diện trắc nghiệm ta dừng lại tại đây (các phương án C và D đương nhiên bị loại).
2. $\bullet\ $  Kết luận có 12 giá trị nguyên của $y$, $y \in \mathbb{N}, 3 \leqslant y\leqslant 14$ thoả ycbt. Nghiệm tăng dần với bước nhảy xấp xỉ $0,4$ nên dự đoán sau 11 lần thực hiện sẽ dừng. Nhưng thực tế bước nhảy giảm nên ta mất 13 bước mới dừng được.

Đón xem chứng minh nếu $y\geqslant 15$ thì phương trình  không có nghiệm trên khoảng $(1;5)$. Đi thi trắc nghiệm không cần chứng minh sự kiện này. Các lời giải của các thầy cô khác cũng chỉ để tham khảo, thí sinh không thể thực hiện phép chứng minh đó trong vòng 9 phút. (với tốc độ trung bình để giải  10 VDC  trong 90 phút).
Tất nhiên cách thực hiện nói trên sẽ không khả thi nếu khoảng chứa nghiệm quá rộng, ví dụ $(1;10)$.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.