BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Một bài toán thực tế hay cho học sinh 12
- 16/06/2021
- 237 lượt xem
Gọi F là một ròng rọc, treo tự do vào cuối sợi dây AF được gắn chặt tại A, và gọi C là quả cân. C được treo ở cuối của sợi dây BFC phía sau ròng rọc F và sợi dây được gắn chặt tại B sao cho các điểm A và B nằm trên cùng một đường ngang. Giả sử rằng ròng rọc và dây thừng có khối lượng không đáng kể. Xác định vị trí của ròng rọc, nghĩa là F ở vị trí nào trong mặt phẳng để $C$ cách đường ngang AB một độ dài lớn nhất.
Áp dụng bằng số $AB=90$cm, AF $= 15$cm.
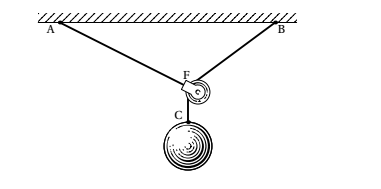
Đây là bài toán kinh điển của phép tính vi tích phân được gọi là “bài toán ròng rọc của Lô-pi-tal” (L’hospital’s Pulley Problem)
GIẢI
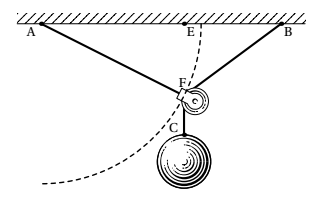Chọn một hệ trục toạ độ $Axy$ gốc $A$, tia $Ax$ đi qua $B$, tia $Ay$ hướng xuống dưới và chọn $15$cm=1 đvd. Khi đó:
$$A(0;0), B(6;0), C(x,y), E(x,0)$$
trong đó $E$ là hình chiếu vuông góc của $F$ trên trục hoành. Như vậy $y=EF+FC$.
Gọi $\ell$ là một số thực sao cho $\ell\times 15$cm là chiều dài của dây thừng BFC (chú ý $\ell$ là hằng số). ta xác định $x$ sao cho $y$ đạt giá trị lớn nhất.
Ta có: $EF=\sqrt{1-x^2}$,
$BF^2=EF^2+EB^2=(1-x)^2+(6-x^2)\Rightarrow BF=\sqrt{37-12x}$.
Vậy $FC= \ell -\sqrt{37-12x}$.
Do đó $y=\sqrt{1-x^2}-\sqrt{37-12x} +\ell $
$y’=-\dfrac{x}{\sqrt{1-x62}}+\dfrac{6}{\sqrt{37-12x}}$
$y’=0\Leftrightarrow 6\sqrt{1-x^2}=x\sqrt{37-12x}$
Bình phương hai vế bằng cách khai triển nhanh trên MTCT
Kết quả ta có phương trình bậc ba $12x^3-73x^2+36=0$
Ta nhận được $x=\dfrac34\Rightarrow C\left(\dfrac34;\dfrac{\sqrt7}{4}\right)$. Bài toán đã được giải xong.
PS. Hình vẽ được viết bằng metapost bởi Sergey Slyurasev. Các thầy cô dạy Vật Lý muốn code mp để biên dịch thành pdf có thể comment ở dưới. Tác giả còn giới thiệu thêm một số hình vẽ vật lý khác trong thư viện của ông, như:
About TS. Nguyễn Thái Sơn
