Giải mã câu 43 chuyên Vinh lần 2

Bài viết này dành cho học sinh khá giỏi, học sinh chuyên toán và giáo viên Toán THPT

Trước hết chúng ta tìm hiểu lời giải truyền thống để hoàn thành câu trắc nghiệm.

Lời giải truyền thống:

$g'(x)=2f'(2x)+4x+2$

$g'(x)=0 \Leftrightarrow f'(2x)+2x+1=0$

Đặt $t=2x+1$, phương trình  trở thành

$f'(t-1)+t=0 \Leftrightarrow f'(t-1)=-t$

Xét đồ thị:

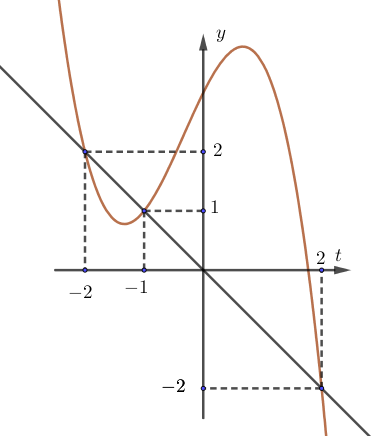
Nhìn vào đồ thị ta thấy nghiệm của phương trình  trên là: $\left[\begin{array}{lrr}
t&=-2&\Rightarrow x=-\dfrac{3}{2}\\
t&=-1&\Rightarrow x=-1\\
t&=2&\Rightarrow x=\dfrac12
\end{array}\right.$

Bảng biến thiên

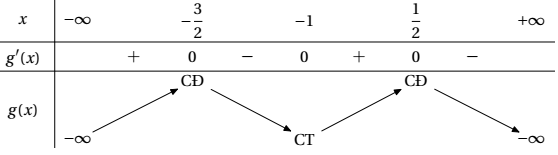
Lưu ý: Do $y=f(x)$ là hàm số bậc 4 (đầy đủ) với $a<0$ nên $g(x)$ cũng là hàm số bậc 4 với $a<0$.

Nhìn vào bảng biến thiên đối chiếu với 4 phương án ta chọn D.

Sau đây chúng ta thử tìm hiểu vì sao tác giả bài toán đặt $g(x)=f(2x)+2x^2+2x$. Muốn vậy ta phục hồi hàm số bậc 4 như đề bài đã nêu.

Theo đề bài ta thấy đồ thị của $f'(x-1)=ax^3+bx^2+cx+d$ đi qua 3 điểm $A(-1;1), B(-2;2), C(2;-2)$ nên ta có hệ phương trình

$$\left\lbrace\begin{array}{ll}
-a+b-c+d&=1\\
-8a+4b-2c+d&=2\\
8a+4b+2c+d&=-2\end{array}
\right.\Leftrightarrow \left\lbrace\begin{array}{llr}
b&=&a\\
c&=&-4a-1\\
d&=&-4a\end{array}
\right.$$

$\Rightarrow f'(x-1)=a(x^3+x^2-4x-4)-x \Rightarrow f'(x)=a(x^3+4x^2+x-6)-x-1$

Bằng cách lấy nguyên hàm ta sẽ tìm được  $f(x)$. Tuy nhiên muốn xác định hàm $f(x)$ cụ thể tác giả bài toán phải cho thêm 2 giả thiết, ví dụ giao của đồ thị của các hàm số $f(x)$ và $f'(x-1)$ với trục tung.

Nhưng ở đây ta muốn tính $g'(x)$  để lập BBT cho hàm số $g(x)$.

Ta có: $g'(x)=2f'(2x)+4x+2=2\left[a(8x^3+16x^2+2x-6)-2x-1\right]+4x+2$

Tóm lại $g'(x)=2a(8x^3+16x^2+2x-6)$

Đến đây vì biết $a<0$ nên ta dễ dàng thiết lập BBT chính là BBT ở trên. Và đây cũng là lý do để tác giả bài toán cộng thêm $2x^2+2x$ vào $f(2x)$ để có một hàm hợp mà có thể lấy được  đạo hàm dễ dàng và lập được  BBT của hàm hợp đó.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.