BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải bài toán niên kim và bài toán trả nợ dần trên máy tính Casio fx-580VN X
- 03/12/2021
- 402 lượt xem
| Đặt vấn đề: Trong Chương trình GDPT mới, môn Toán lớp 12 sẽ có một chuyên đề về Toán tài chính. Thực ra đây là vấn đề mở rộng của bài toán lãi suất mà trong nhiều năm qua học sinh đã học và luyện tập nâng cao với bài toán lãi kép coi như một ứng dụng của hàm số mũ. Ngoài ra trong nhiều đề thi thử của một số trường THPT chuyên cũng có nhiều bài toán phong phú về dạng này. Để có thêm tư liệu cho HS học tập và GV tham khảo chúng tôi biên soạn lại bài toán niên kim. |
Bài toán niên kim gần như là bài toán ngược của bài toán trả nợ dần.
- 1. Với bài toán trả nợ dần ta vay ở ngân hàng một khoản $P$ với lãi suất $i$ và mỗi tháng (giả sử vào cuối tháng) trong $n$ tháng ta nộp vào ngân hàng một khoản $R$ cho đến khi kết thúc hợp đồng.
- 2. Với bài toán niên kim, mỗi tháng (giả sử vào cuối tháng) ta nộp vào ngân hàng một khoản là $R$ với lãi suất $i$ thì sau $n$ tháng ta sẽ nhận được một khoản là $F$.
Thông thường bài toán niên kim cho ba trong bốn giá trị $R, n, i, F/P$ yêu cầu tìm giá trị thứ tư.
Công thức cho bài toán niên kim như sau
$$F=\dfrac{R}{i}((1+i)^n-1)$$
Nếu đề bài cho $P$ thì ta thay $F=P(1+i)^n$, trong đó $R$ là số tiền nộp hàng tháng, $i$ lãi suất tính theo tháng, $n$ là số tháng thực hiện việc nộp tiền.
|
Ví dụ 1: Một cặp vợ chồng trẻ vừa hạ sinh một bé gái. Họ có kế hoạch tiết kiệm để cháu bé có một khoản học phí theo học đại học. Họ mở một tài khoản tiết kiệm ở ngân hàng và nộp $200 vào cuối mỗi tháng với lãi kép 2.7%/năm. Hỏi mười tám năm sau, sau 216 lần nộp tiền, giá trị tương lai của tài khoản tiết kiệm nói trên là bao nhiêu? |
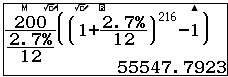
| Ví dụ 2: Một người trúng số độc đắc, anh ta quyết định nghỉ làm việc trong 5 năm. Anh ta muốn nộp vào ngân hàng một khoản tiền để có thể rút ra $5000 vào cuối mỗi tháng trong 60 tháng. Ngân hàng ấn định lãi kép 2.1% hàng tháng. Hỏi số tiền anh ta phải nộp là bao nhiêu? |
Lưu ý: lãi kép 2.1% hàng tháng (theo thuật ngữ của sách GK tại Hoa Kỳ) nghĩa là lãi kép 2.1%/năm với kỳ hạn là tháng.
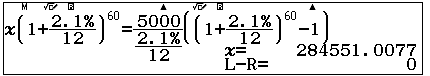
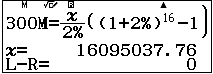
| Ví dụ 3: Anh A còn 8 năm nữa để làm việc. Anh muốn khi nghỉ hưu sẽ mua một chiếc xe hơi trị giá 300.000.000 VNĐ. Anh ấy gửi vào một tài khoản tiết kiệm ở ngân hàng với lãi kép 4% bán niên trong 8 năm, cứ cuối mỗi 6 tháng nộp tiền một lẩn. Hỏi mỗi lần nộp tiền, anh A phải nộp bao nhiêu để đủ tiền mua chiếc xe hơi nói trên. |
Chú ý: lãi kép 4% bán niên nghĩa là lãi kép 4%/năm với kỳ hạn là bán niên (6 tháng).
Vậy lãi kép là 2%/bán niên (2% mỗi bán niên).
| Ví dụ 4: Tom cần mua căn nhà có giá trị $\$300,000$ và anh ta cần đặt cọc trước 10% tổng giá trị đó và sẽ trả 90% còn lại trong vòng 30 năm với lãi kép 8%/năm. Vậy số tiền cần đặt đợt đầu là $\$30,000$ và số dư nợ còn lại là $270,000. Hỏi mỗi tháng Tom phải trả ngân hàng bao nhiêu? |
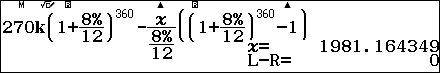
| Lưu ý: Trong bài toán trả nợ dần trong hai ví dụ trên, kỳ hạn trả nợ là phải nói rõ (đóng hàng tháng, hàng quý, bán niên hay thậm chí hàng năm). Nếu không nói rõ mà đề bài yêu cầu “mỗi tháng đóng bao nhiêu” thì ta quy ước kỳ hạn là tháng. |
About TS. Nguyễn Thái Sơn
