Các bài toán về nhị thức Newton
- 14/02/2022
- 277 lượt xem
| Ghi nhớ: $\quad C^k_n$ là tích của $k$ số tự nhiên liên tiếp bắt đầu từ $n$ hạ xuống và chia cho $k!$. Như vậy: $$C^1_n=n\quad ;\quad C^2_n=\dfrac{n(n-1)}{2!}\quad , \quad C^3_n=\dfrac{n(n-1)(n-2)}{3!}\quad ; \quad C^4_n=\dfrac{n(n-1)(n-2)(n-3)}{4!}$$ |
| Công thức nhị thức Newton: $$(a+b)^n=\sum_{k=1}^{n}C^k_na^{n-k}b^k$$
Nếu $a=\alpha x^{p}\ ; b=\beta x^{q}$ thì biểu thức $a^{n-k}b^k$ trở thành $\large \alpha^{n-k}\beta^{k}x^{p(n-k)+qk}$.
Số $$p(n-k)+qk$$ được gọi là số mũ của số hạng tổng quát, trong đó $p,q,n$ đã cho và $k$ là số cần tìm. Để tìm $k$ ta giải phương trình $$p(n-x)+qx=r$$ với $r$ là số mũ mà đề bài yêu cầu.
Khi đó hệ số của số hạng chứa $x^r$ là $\large C^k_n\alpha^{n-k}\beta^k$. |
Áp dụng vào bài toán đã nêu với $\alpha = 1, \beta=2, p=3, q=-2, r=0$:
Tìm $n\quad $ 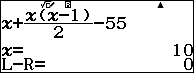
Tìm $k\quad $ 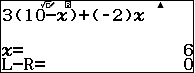
Vậy số hạng không chứa $x$ là 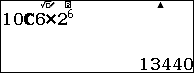

Với $(2x-1)^6$ ta có $\alpha=2,p=1,\beta=-1,q=0,r=4,n=6$ suy ra $k=\quad $ 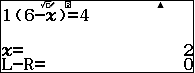
Với $(3x-1)^8$ ta có $\alpha=3,p=1,\beta=-1,q=0,r=5,n=8$ suy ra $k=\quad $ 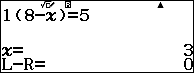
Vậy hệ số của số hạng chứa $x^5$ là 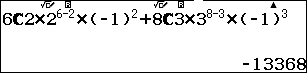
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay