Lại nói về tứ giác nội tiếp
- 03/05/2023
- 109 lượt xem
Chúng ta dựa vào đề thi vào lớp 10 chuyên SGD Hà Nội năm 2021

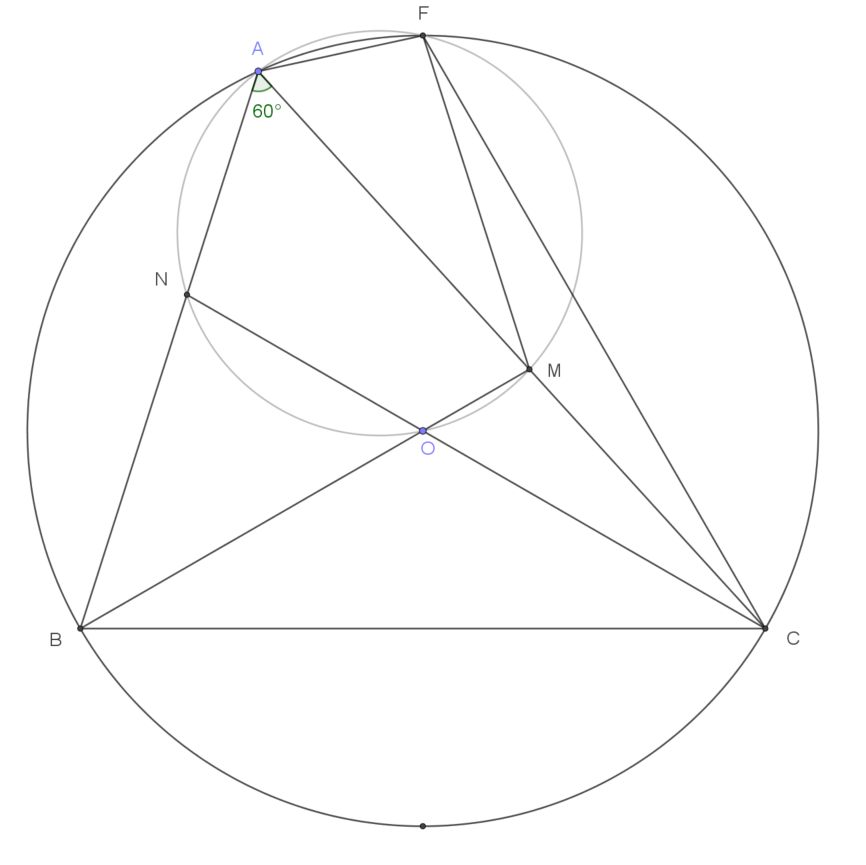
a) Chứng minh 5 điểm $A, N, O, M, F$ cùng nằm trên một đường tròn.
| Vì $F$ là điểm chính giữa của cung lớn $BC$ nên $FB=FC$, ngoài ra $\widehat{BFC}=\widehat{BAC}=60^\circ$ nên tam giác $FBC$ là tam giác đều. Mà $O$ là tâm đường tròn ngoại tiếp nên $BO$ là đường trung trực của $FC$. Điểm $M$ nằm trên đường trung trực của $FC$ nên $MF=MC$, nghĩa là tam giác $MFC$ cân tại $M$, Do đó $\widehat{FMA}=2 \widehat{FCM}=\widehat{AOF}$ (góc nội tiếp và góc ở tâm cùng chắn cung).
Vậy tứ giác $AOMF$ nội tiếp. Tứ giác $AMON$ có $\widehat{MAN}+\widehat{MON}= \widehat{MAN}+\widehat{BOC}=60^\circ +120^\circ=180^\circ$ nên cũng là tứ giác nội tiếp. Tóm lại 5 điểm $A, N, O, M, F$ cùng nằm trên một đường tròn, đó là đường tròn ngoại tiếp tam giác $AMO$ . (đpcm) |
b) Chứng minh $AJ$ là tia phân giác của góc $\widehat{BAC}$.
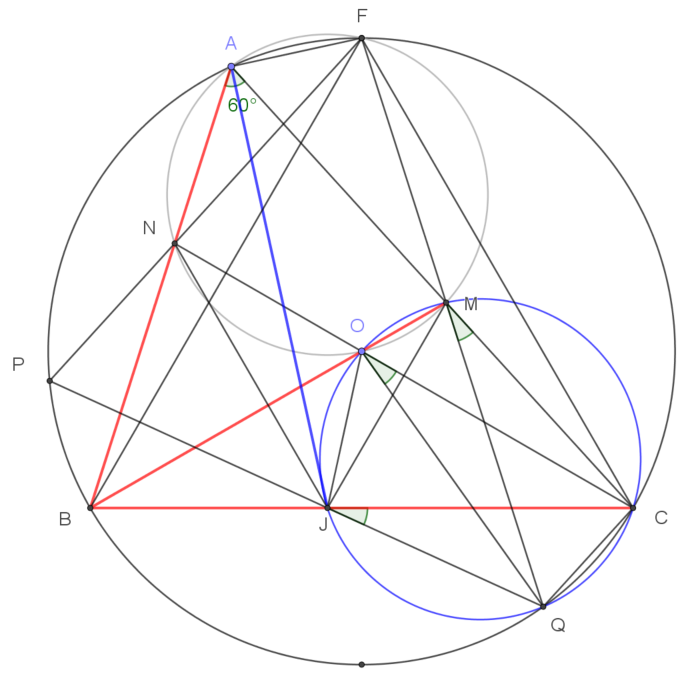
| Chứng minh tương tự như trên tam giác $NBC$ cân tại $N$. Suy ra $\widehat{NFB}=\widehat{NBF}$, $\widehat{NBF}=\widehat{MCF}$ (cùng chắn cung $AF$), $\widehat{MCF}=\widehat{MFC}$ (chứng minh trên). Từ đó suy ra $\widehat{PFB}=\widehat{QFC} ⇒ \text{cung}\ BP =\text{cung}\ QC$.
$\widehat{CJQ}=\dfrac{\text{sđ cung}\ BP +\text{sđ cung}\ CQ}{2}=\text{sđ cung}\ CQ $ $\widehat{CJQ}=\widehat{COQ}$ (số đo của góc ở tâm bằng số đo của cung bị chắn.) $\widehat{COQ}=2 \widehat{CFQ}$ (góc nội tiếp và góc ở tâm cùng chắn cung) $2\widehat{CFQ}=\widehat{CMQ}$. Tóm lại $\widehat{CJQ}=\widehat{COQ}=\widehat{CMQ}$ suy ra 5 điểm $M, O, J, Q, C$ cùng nằm trên một đường tròn , đó là đường tròn ngoại tiếp tam giác $COQ$.
Xét đường tròn ngoại tiếp tam giác $AMO$, hai cát tuyến $BMA$ và $BOM$ cho ta $BN.BA=BO.BM$ (do hai tam giác $BNO$ và $BMA$ đồng dạng ).
Xét đường tròn ngoại tiếp tam giác $COQ$, hai cát tuyến $BJC$ và $BOM$ cho ta $BJ.BC=BO.BM$ (do hai tam giác $BOQ$ và $BCM$ đồng dạng).
Vậy $BN.BA=BJ.BC$, suy ra tứ giác $ANJC$ nội tiếp. Do đó $\widehat{NAJ}=\widehat{NCJ}=30^\circ$, suy ra $AJ$ là tia phân giác của góc $BAC$. |
| Nhận xét: Khi ta có $BN.BA=BJ.BC$ ta suy ra hai tam giác $BNJ$ và $BCA$ đồng dạng, suy ra $\widehat{BNJ}=\widehat{BCA}$, đây là lý do tứ giác nội tiếp. |
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay