BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Về việc chứng minh trung điểm của một đoạn thẳng
- 10/01/2023
- 68 lượt xem
Một số bài toán chứng minh trung điểm của một đoạn thẳng khá phức tạp. Những ví dụ sau đây nhằm tìm ra một Phương pháp chung để thực hiện việc chứng minh đó.
| Ví dụ 1: Cho một điểm $M$ nằm ngoài đường tròn $(O)$. Qua $M$ vẽ hai tiếp tuyến $MA, MB$ với $A$ và $B$ là hai tiếp điểm. Vẽ cát tuyến $MCD$ sao cho $C$ nằm giữa $M$ và $D$. Vẽ đường kính $BE$. Qua $C$ vẽ một đường thẳng song song với $MO$ cắt $ED$ và $EB$ lần lượt tại $P$ và $I$. Chứnh minh $I$ là trung điểm $CP$. |
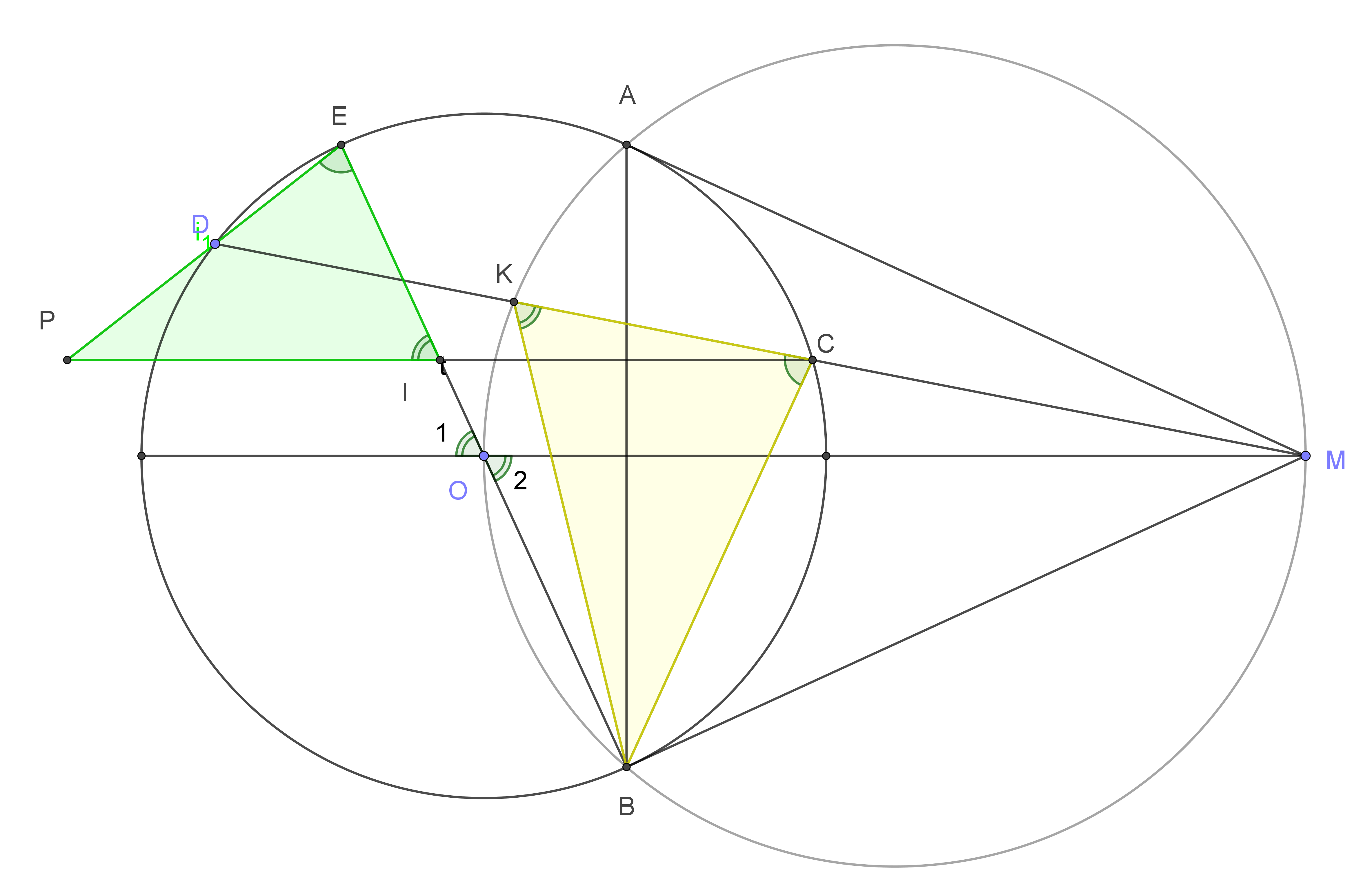
Gọi $K$ là trung điểm $CD$. Ta chứng minh tam giác $EIP$ đồng dạng với tam giac $CKB$.
Thật vậy,
$\widehat{EIP}=\widehat{O_1}$ (đồng vị)
$\widehat{O_1}=\widehat{O_2}$ (đối đỉnh)
$\widehat{O_2}=\widehat{BKM}$ (cùng chắn cung $BM$ của đường tròn đi qua 5 điểm M, O, A, B, K).
Suy ra $\widehat{EIP}=\widehat{BKC}\quad (1)$.
$\widehat{DEB}=\widehat{KCB}$ (cùng chắn cung $DB$) (2)
Từ (1) và (2) ta có: $\Delta EIP \backsim \Delta CKB$.
Suy ra $\dfrac{IP}{KB}=\dfrac{IE}{KC} \Rightarrow IP=\dfrac{KB.IE}{KC}$
Chứng minh tương tự ta có: $\Delta IEC\backsim \Delta KDB$
Suy ra $\dfrac{IC}{KB}=\dfrac{IE}{KD}\Rightarrow IC=\dfrac{KB.IE}{KD}$
Vì $KC=KD$ nên $IP=IC$ (đpcm).
| Ví dụ 2:
Xem bài hàng điểm điều hòa |
About TS. Nguyễn Thái Sơn
