BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Về bài toán tứ giác nội tiếp trong đề thi Toán chuyên TPHCM năm 2022 (phần 2)
- 06/03/2023
- 100 lượt xem
| Trong phần đầu, chúng tôi hướng dẫn học sinh chứng minh $M$ là trung điểm $BC$ thông qua một đẳng thức đã được chứng minh ở câu 1. Trong phần này chúng tôi hướng dẫn các em chứng minh trực tiếp sự kiện đó. |
| Bài toán: Cho tam giác $ABC$ nhọn $AB<AC$ có các đường cao $AD, BE, CF$ cắt nhau tại $H$. Đường thẳng $EF$ cắt $BC$ tại $I$. Đường thẳng qua $A$ và vuông góc với $IH$ tại $K$ cắt đường thẳng BC tại $M$. Chứng minh $M$ là trung điểm $BC$. |
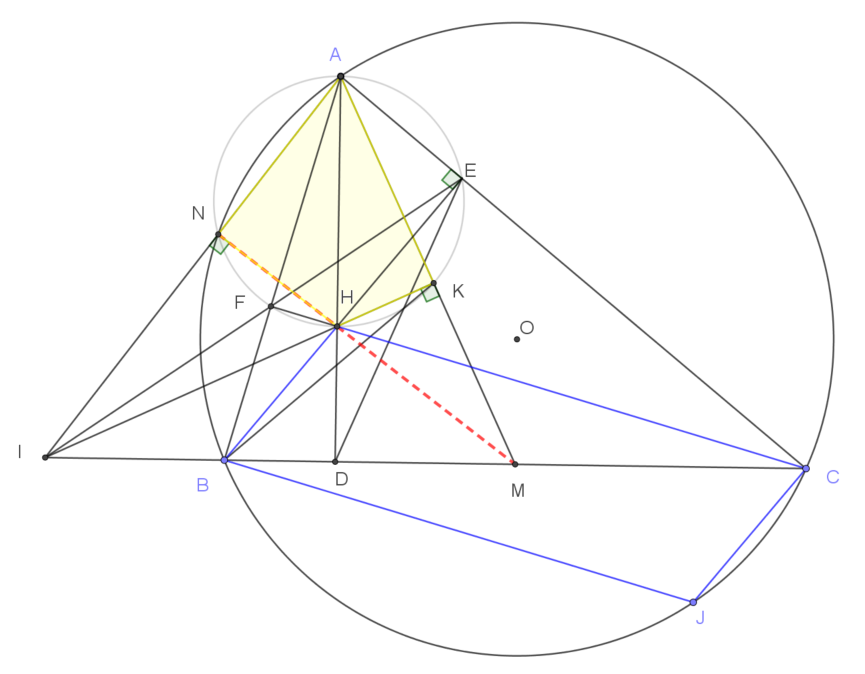
Gọi $N$ là giao điểm (thứ hai) của đường thẳng $AI$ và đường tròn $(O)$. Vẽ đường kính $AJ$ của đường tròn $(O)$.
- $\color{red}\bullet$ Ta có $IN.IA=IB.IC$ (hệ thức lượng trong đường tròn $(O)$).
$\qquad \quad IB.IC=IF.IE$ (hệ thức lượng trong đường tròn đường kính $BC$).
$\qquad \quad IF.IE=IH.IK$ (hệ thức lượng trong đường tròn đường kính $AH$).
Vậy $IN.IA=IH.IK$ do dó tứ giác $ANHE$ nội tiếp, mà $\widehat{AKH}=90^\circ$ nên $\widehat{ANH}=90^\circ$ nên $HN\perp AI\quad (1)$
- $\color{blue}\bullet$ Tam giác $AIM$ nhận $H$ làm trực tâm nên $MH\perp AI\quad (2)$
Từ (1) và (2) suy ra $N, H, M$ thẳng hàng.
- $\color{magenta}\bullet$ Tam giác $ANJ$ nội tiếp đường tròn đường kính $AJ$ nên là tam giác vuông tại $N$. Do đó $JN\perp AI$, suy ra 4 điểm $N, H, M, J$ thẳng hàng.
Tứ giác $BHCJ$ là hình bình hành, hai đường chéo $BC$ và $HJ$ cắt nhau tại $M$ nên $M$ là trung điểm $BC$.
| Lưu ý: Việc sử dụng hệ thức lượng trong đường tròn là KHÔNG KHUYẾN KHÍCH dành cho bài thi tuyển sinh 10. Tuy nhiên đối với bài thi chuyên đôi khi phải sử dụng. Việc chứng minh hệ thức đó không khó vì ta thấy ngay hai tam giác đồng dạng có liên quan. Và trong cùng một bài, việc chứng minh hệ thức lượng này chỉ thực hiện một lần, những lần sau (nếu có) sẽ nói là “tương tự. “ |
Chia sẻ
About TS. Nguyễn Thái Sơn
