ỨNG DỤNG MÁY TÍNH CASIO FX-580VN X VÀO CÁC BÀI TOÁN THỰC TẾ PT & HPT DÀNH CHO ÔN THI TUYỂN SINH LỚP 10
- 20/04/2021
- 651 lượt xem
Bài 1: Một xe ô tô dự định đi từ Tp Hồ Chí Minh đến Bà Rịa- Vũng Tàu cách nhau 120km trong một thời gian đã định. Sau khi đi được 1 giờ sẽ dừng lại nghỉ 10 phút rồi tiếp tục đi và tăng vận tốc thêm 6km/h để đền Bà Rịa- Vũng Tàu đúng giờ đã định. Tính vận tốc ban đầu của ô tô.
Hướng dẫn: Đổi 10 phút = giờ
Gọi vận tốc ban đầu của ô tô là x (km/h) (Điều kiện x>0)
Sau 1 giờ ô tô đi được quãng đường dài x.1 = x(km)
Quãng đường ô tô đi được với vận tốc x+6(km/h) là 120-x (km)
Theo đề bài ta có phương trình:
(nhận) ;
(loại)
Sử dụng máy tính:
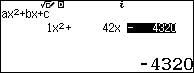
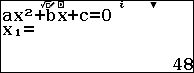
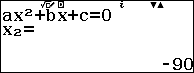
Vậy vận tốc ban đầu của ô tô là 48(km/h)
Bài 2: Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Tâm rủ nhau đi uống nước mía ở một quán trước cổng trường. Nhân dịp sinh nhật lần thứ 3 của quán nên có khuyến mãi, bắt đầu mua ly thứ 3 giá mỗi ly nước mía giảm 3 000 đồng so với giá ban đầu. Nhóm Tâm mua 8 ly nước mía với số tiền là 78 000 đồng. Hỏi giá của một ly nước mía ban đầu?
Hướng dẫn: Gọi x(đồng) là giá ly nước mía ban đầu.
Theo giả thiết ta có phương trình: 2x+6(x-3000)=78000
(đồng)
Sử dụng máy tính:

Vậy giá tiền của một ly nước mía là 12 000 đồng
Bài 3: Một chiếc thuyền xuôi dòng, ngược dòng trên khúc sông dài 40km hết 4h30 phút. Biết thời gian xuôi dòng 5km bằng thời gian thuyền ngược dòng 4km. Tính vận tốc dòng nước.
Hướng dẫn: Gọi vận tốc của thuyền khi nước yên lặng là x km/h
Gọi vận tốc dòng nước là y km/h (đk x>y>0)
Vì thời gian thuyền xuôi dòng 5km bằng thời gian thuyền ngược dòng 4km nên ta có phương trình: (1)
Vì chiếc thuyền xuôi ngược dòng trên khúc sông dài 40km hết 4h30 phút nên ta có phương trình: (2)
Từ (1) và (2) ta có hệ :
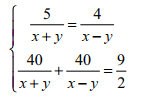
Giải ra ta được vận tốc của thuyền là 18km/h và vận tốc của dòng nước là 2km/h
Sử dụng máy tính:
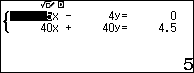


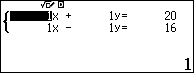


Bài 4: Một phòng họp có 100 chỗ ngồi, nhưng số người đến họp là 144. Do đó, người ta phải kê thêm 2 dãy ghế và mỗi dãy ghế phải thêm 2 người ngồi. Hỏi phòng họp lúc đầu có mấy dãy ghế?
Hướng dẫn: Gọi số dãy ghế lúc đầu là x ( dãy), x nguyên dương.
Số dãy ghế sau khi thêm là: x + 2 (dãy).
Số ghế của một dãy lúc đầu là: (ghế)
Số ghế của một dãy sau khi thêm là: (ghế)
Vì mỗi dãy ghế phải thêm 2 người ngồi nên ta có phương trình:
Giải phương trình ta được x=10 (thỏa mãn đk)
Vậy phòng họp lúc đầu có 10 dãy ghế.
Sử dụng máy tính:
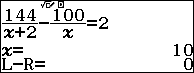
Bài 5: Bà Nga gửi 800000000 đồng vào ngân hàng với lãi suất kì hạn 1 năm. Sau 2 năm bà Nga nhận được số tiền cả vốn lẫn lãi là 907380000 đồng. Hỏi lãi xuất ngân hàng đó là bao nhiêu phần trăm trong 1 năm? Biết rằng số tiền lãi của năm đầu được gộp vào vốn để tính lãi cho năm sau.
Hướng dẫn: Gọi lãi suất ngân hàng đó là x% (đk x>0)
Số tiền nhận cả vốn lẫn lãi sau 1 năm :
800000000+ 800000000. x%= 800000000 (1+x%) (đồng)
Sau 2 năm nhận cả vốn lẫn lãi là:
800000000 (1+x%)+800000000 (1+x%).x%= (đồng)
Khi đó ta có phương trình:
(nhận) ;
(loại)
Sử dụng máy tính:
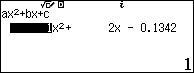
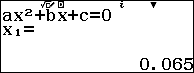
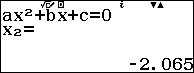
Vậy lãi suất của ngân hàng đó là 6,5%
Bài 6: Hai người thợ cùng sơn cửa cho một ngôi nhà thì 2 ngày xong việc. Nếu người thứ nhất làm trong 4 ngày rồi nghỉ người thứ hai làm tiếp trong 1 ngày nữa thì xong việc. Hỏi mỗi người làm một mình thì bao lâu xong công việc?
Hướng dẫn: Gọi thời gian để một mình người thứ nhất hoàn thành công việc là x (x>2; ngày)
Gọi thời gian để một mình người thứ hai hoàn thành công việc là y (x>2; ngày).
Trong một ngày người thứ nhất làm được công việc
Trong một ngày người thứ hai làm được công việc
Cả hai người làm xong trong 2 ngày nên trong 1 ngày cả hai người làm được công việc. Từ đó ta có phương trình
(1)
Người thứ nhất làm trong 4 ngày rồi người thứ hai làm trong 1 ngày thì xong công việc ta có phương trình (2)
Từ (1) và (2) ta có hệ phương trình:
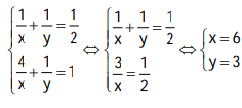
Vậy người thứ nhất làm một mình xong công việc trong 6 ngày. Người thứ hai làm một mình xong công việc trong 3 ngày.
Sử dụng máy tính:
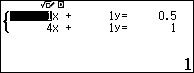


Bài 7: Đội sản xuất phải làm 75 sản phẩm trong thời gian quy định. Nhờ tăng năng suất lao động, nên mỗi ngày đội làm thêm được 5 sản phẩm so với kế hoạch. Vì vậy chẳng những đã làm vượt mức kế hoạch 5 sản phẩm mà còn hoàn thành công việc sớm hơn dự tính một ngày. Tính số sản phẩm mà đội phải làm trong một ngày theo kế hoạch.
Hướng dẫn: Gọi số sản phẩm mà xí nghiệp phải làm mỗi ngày theo kế hoạch là x (đk x
)
Thời gian hoàn thành theo kế hoạch là (ngày)
Thực tế mỗi ngày xí nghiệp làm được x+5 ( sản phẩm)
Thời gian hoàn thành trong thực tế là ( ngày)
Vì thực tế xí nghiệp hoàn thành sớm hơn 1 ngày so với kế hoạch nên ta có phương trình:
Biến đổi được phương trình ta được:
(nhận) ;
(loại)
Vậy theo kế hoạch, mỗi ngày xí nghiệp sản xuất 15 sản phẩm
Sử dụng máy tính:

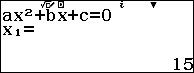
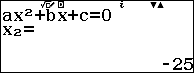
Bài 8: Cho quãng đường AB dài 120 km. Lúc 7h sáng một xe máy đi từ A đến B. Đi được xe bị hỏng phải dừng lại 10 phút để sửa rồi đi tiếp với vận tốc kém vận tốc ban đầu 10km/h. Biết xe máy đến B lúc 11h40 phút trưa cùng ngày. Giả sử vận tốc xe máy trên
quãng đường đầu không đổi và vận tốc xe máy trên
quãng đường còn lại cũng không đổi. Hỏi xe máy bị hỏng lúc mấy giờ?
Hướng dẫn: Gọi vận tốc trên quãng đường ban đầu là x (km/h) x>10
Thì vận tốc trên quãng đường sau là x-10 (km/h)
Thời gian đi trên quãng đường ban đầu là
(h)
Thời gian đi trên quãng đường sau là
(h)
Vì thời gian đi cả 2 quãng đường là 11h40 phút -7h-10 phút= (h)
Nên ta có pt:
( loại);
(nhận)
Thời gian đi trên quãng đường ban đầu
= 3(h)
Vậy xe hỏng lúc 10h
Sử dụng máy tính:


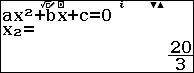
Bài 9: Khi thêm 200g Axít vào dung dịch Axít thì dung dịch mới có nồng độ Axít là 50%. Lại thêm 300 gam nước vào dung dịch mới, ta được dung dịch Axít có nồng độ là 40%. Tính nồng độ Axít trong dung dịch đầu tiên.
Hướng dẫn: Khối lượng nước trong dung dịch đầu tiên là x gam, khối lượng Axít trong dung dịch đầu tiên là y gam .
Sau khi thêm, 200 gam Axít vào dung dịch Axít ta có lượng Axít là:(y+200) gam và nồng độ là 50%.
Do đó ta có:
(1)
Sau khi thêm 300 gam nước vào dung dịch thì khối lượng nước là: (x+300) gam và nồng độ là 40% (=2/5) nên ta có:
(2)
Giải hệ (1) và (2) ta được x=600; y=400.
Vậy nồng độ Axít là: .100 = 40
Sử dụng máy tính:
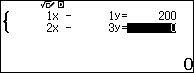


Bài 10: Trong túi đựng bi đỏ và bi xanh. Nếu lấy ra một bi đỏ thì một phần bảy số bi còn lại là đỏ. Nếu lấy ra hai bi xanh thay vì một bi đỏ thì một phần năm số bi còn lại là đỏ. Hỏi trong túi lúc đầu có bao nhiêu bi đỏ và bao nhiêu bi xanh?
Hướng dẫn: Gọi số bi đỏ có trong túi lúc đầu là x, x>1
Gọi số bi xanh có trong túi lúc đầu là y, y>2
Nếu lấy ra một bi đỏ thì một phần bảy số bi còn lại là đỏ nên:
Nếu lấy ra hai bi xanh thay vì một bi đỏ thì một phần năm số bi còn lại là đỏ nên:
Vậy ta có hệ phương trình:
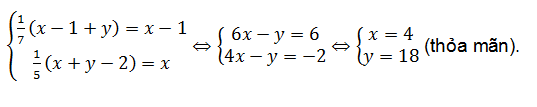
Vậy trong túi lúc đầu có 4 bi đỏ và 18 bi xanh.
Sử dụng máy tình:
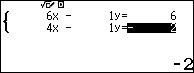


 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay