BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Ưu thế của phương pháp lập bảng giá trị (Table)
- 03/08/2022
- 850 lượt xem
|
Giải
- 1. Ta xét tất cả các số có dạng $\overline{773abcd9}$ bắt đầu từ $\overline{77300009}$ đến $\overline{77399999}$.Ta có nhận xét
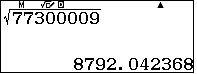
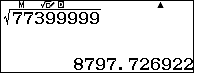.Vậy các số cần tìm là bình phương của một số nguyên từ $8793$ đến $8797$.Lập bảng giá trị của hàm số $f(x)=x^2$ với $x$ nguyên từ $8793$ đến $8797$ ta có bảng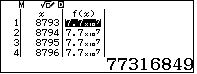
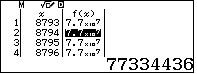
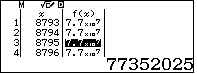
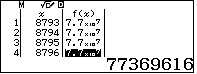
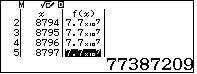Quan sát ta thấy có hai số thỏa ycbt là 1684, 8720. - 2. Ta có $x^3 +3xy^2+ y^2=144861\Leftrightarrow y=\sqrt{\dfrac{144861-x^3}{3x+1}}
.$
Do $y>0$ nên $x<$
.Lập bảng giá trị cho hàm số 
.Lần đầu cho $x$ chạy từ $1$ đến $45$, sau đó cho $x$ chạy từ $46$ đến $53$, ta có hao giá trị của
$y$ và tương ứng với hai giá trị của $x$ là: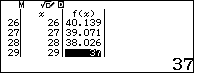
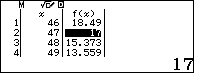Vậy ta có hai cặp số nguyên dương $x, y$ thỏa yêu cầu bài toán là
$$x=47, y=17 \quad \text{và}\quad x=29, y=37$$
Chia sẻ
About TS. Nguyễn Thái Sơn
