GIẢI QUYẾT CÁC BÀI TOÁN VIET VỚI CASIO fx- 580VN X
- 27/12/2021
- 2,053 lượt xem
Trong bài viết dưới đây, Diễn đàn sẽ tổng hợp một số kiến thức cần nhớ về định lý Viete và một số bài toán minh họa nhằm giúp các bạn học sinh có thể ôn tập và rèn luyện thêm
I. KIẾN THỨC CHUNG
Phương trình bậc hai đối với ẩn $x\in R$ là phương trình có dạng: $\text{a}{{\text{x}}^{\text{2}}}+bx+c=0\left( 1 \right)\quad \left( a\ne 0 \right)$
Cách giải.
- Tính $\Delta ={{b}^{2}}-4ac$
Nếu $\Delta <0$ thì phương trình (1) vô nghiệm.
Nếu $\Delta =0$ thì phương trình (1) có nghiệm kép ${{x}_{1}}={{x}_{2}}=-\frac{b}{2a}$.
Nếu $\Delta >0$ thì phương trình (1) có hai nghiệm phân biệt ${{x}_{1}}=\frac{-b-\sqrt{\Delta }}{2a},\ \ {{x}_{2}}=\frac{-b+\sqrt{\Delta }}{2a}$
Định lý Vi-et – Dấu các nghiệm.
-
- Định lý: Nếu phương trình bậc hai ẩn $x\in R$: $\text{a}{{\text{x}}^{\text{2}}}+bx+c=0\left( 1 \right)\quad \left( a\ne 0 \right)$ có hai nghiệm ${{x}_{1}},\ \ {{x}_{2}}$ thì $S={{x}_{1}}+{{x}_{2}}=\frac{-b}{a},\ \ P={{x}_{1}}.{{x}_{2}}=\frac{c}{a}$.
- Dấu các nghiệm:
+ Phương trình (1) có hai nghiệm trái dấu $\Leftrightarrow P<0$.
+ Phương trình (1) có hai nghiệm cùng dấu $\Leftrightarrow\left\{\begin{align}& \Delta \ge 0 \\ & P>0 \\ \end{align} \right.$.
+ Phương trình (1) có hai nghiệm cùng dương $\Leftrightarrow \left\{\begin{align}& \Delta \ge 0 \\ & P>0 \\ & S>0 \\ \end{align} \right.$.
+ Phương trình (1) có hai nghiệm cùng âm $\Leftrightarrow \left\{\begin{align}& \Delta \ge 0 \\ & P>0 \\ & S<0 \\ \end{align} \right.$.
II. MỘT SỐ BÀI TOÁN MINH HỌA
Bài 1. Cho phương trình ${{x}^{4}}-2\left( m-2 \right){{x}^{2}}+2m-6=0$. Tìm các giá trị của m sao cho phương trình có 4 nghiệm phân biệt.
Hướng dẫn giải
${{x}^{4}}-2\left( m-2 \right){{x}^{2}}+2m-6=0$ (1)
Đặt $t={{x}^{2}}\left( t\ge 0 \right)$
(1) $\Leftrightarrow $ ${{t}^{2}}-2\left( m-2 \right)t+2m-6$ (2)
${\Delta }’={{\left( m-2 \right)}^{2}}-\left( 2m-6 \right)={{m}^{2}}-6m+10={{\left( m-3 \right)}^{2}}+1>0$
Kiểm tra bằng máy tính Casio fx- 580VN X:
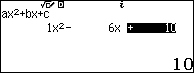
Phương trình (2) luôn có 2 nghiệm phân biệt.
Ứng với mỗi nghiệm $t\text{ }>\text{ }0$ thì phương trình (1) có 2 nghiệm phân biệt. Do đó, phương trình (1) có 4 nghiệm phân biệt khi chỉ khi phương trình (2) có hai nghiệm phân biệt dương.
$\Leftrightarrow $ $2m-6>0$ và $2\left( m-2 \right)>0$$\Leftrightarrow $ $m\text{ }>\text{ }3$.
Vậy $m\text{ }>\text{ }3$ thỏa mãn yêu cầu.
Bài 2. Cho phương trình ${{x}^{2}}-2\left( m-1 \right)x+{{m}^{2}}-6=0$ (1) (với $m$ là tham số).
a) Giải phương trình với $m=3.$
b) Với giá trị nào của $m$ thì phương trình (1) có các nghiệm ${{x}_{1}},\,\,{{x}_{2}}$ thỏa mãn $x_{1}^{2}+x_{2}^{2}=16$
Hướng dẫn giải
a) Với $m=3$, ta có phương trình (1) trở thành ${{x}^{2}}-4x+3=0$
Ta có $a+b+c=1-4+3=0$ nên phương trình có 2 nghiệm phân biệt ${{x}_{1}}=1;\,\,{{x}_{2}}=3$
Vậy với $m=3$, phương trình đã cho có 2 nghiệm phân biệt ${{x}_{1}}=1;\,\,{{x}_{2}}=3$
b) ${{x}^{2}}-2\left( m-1 \right)x+{{m}^{2}}-6=0$ (1)
Phương trình (1) là phương trình bậc 2 ẩn $x$ có $\Delta ‘={{\left( m-1 \right)}^{2}}-\left( {{m}^{2}}-6 \right)=7-2m$
Phương trình (1) có các nghiệm ${{x}_{1}},\,\,{{x}_{2}}\,\,\Leftrightarrow \,\,\Delta ‘\ge 0\,\,\Leftrightarrow \,\,7-2m\ge 0\,\,\Leftrightarrow \,\,m\le \frac{7}{2}$ (*)
Khi đó theo định lý Viét ta có ${{x}_{1}}+{{x}_{2}}=2\left( m-1 \right);\,\,\,{{x}_{1}}.{{x}_{2}}={{m}^{2}}-6$
Do đó $x_{1}^{2}+x_{2}^{2}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}}=4{{\left( m-1 \right)}^{2}}-2\left( {{m}^{2}}-6 \right)=2{{m}^{2}}-8m+16$
Vậy $x_{1}^{2}+x_{2}^{2}=16\Leftrightarrow 2{{m}^{2}}-8m+16=16\,\,\Leftrightarrow \,\,\left[ \begin{align}& m=0 \\ & m=4 \\ \end{align} \right.$
Kết hợp điều kiện (*) ta có $m=0$ là giá trị thỏa mãn.
Sử dụng Casio fx- 580VN X để kiểm tra đáp án
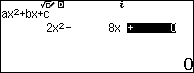
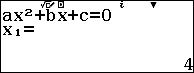
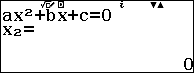
Bài 3.
a) Chứng minh phương trình ${x}^2-2x-2=0$ có hai nghiệm phân biệt${{x}_{1}},{{x}_{2}}$.
Tính $T=2{{x}_{1}}+{{x}_{2}}\left( 2-3{{x}_{1}} \right)$.
b) Chứng minh ${{x}^{2}}-3x+5>0$, với mọi số thực $x$.
Hướng dẫn giải
a. Chứng minh phương trình ${{x}^{2}}-x-2=0$ luôn có 2 nghiệm phân biệt:
$\Delta ‘=b{{‘}^{2}}-ac={{\left( -1 \right)}^{2}}-1\left( -2 \right)=3\Rightarrow \Delta ‘>0$ nên phương trình luôn có 2 nghiệm phân biệt.
${{x}_{1}}+{{x}_{2}}=2$, ${{x}_{1}}{{x}_{2}}=-2$
Tính
$T=2{{x}_{1}}+{{x}_{2}}\left( 2-3{{x}_{1}} \right)=2\left( {{x}_{1}}+{{x}_{2}} \right)-3{{x}_{1}}{{x}_{2}}=2\left( -2 \right)-3\left( -2 \right)=10$
b. Chứng minh ${{x}^{2}}-3x+5>0$ với mọi x
Ta có: ${{x}^{2}}-3x+5={{x}^{2}}-2x.\frac{3}{2}+{{\left( \frac{3}{2} \right)}^{2}}-{{\left( \frac{3}{2} \right)}^{2}}+5={{\left( x-\frac{3}{2} \right)}^{2}}+\frac{11}{4}>0$
Kiểm tra lại bằng Casio fx- 580VN X
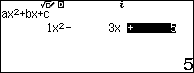
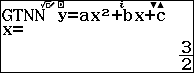
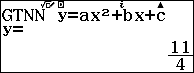
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay