BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG MÁY TÍNH FX-880BTG TÌM ƯỚC CHUNG LỚN NHẤT VÀ BỘI CHUNG NHỎ NHẤT
- 07/09/2022
- 5,454 lượt xem
1. Cách tìm ước chung lớn nhất -ƯCLN.
Muốn tìm ƯCLN của hai hay nhiều số lớn hơn $1$, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, Mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN cần tìm
Lưu ý:
Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng $1$.
Hai hay nhiều số có ƯCLN bằng $1$ gọi là các số nguyên tố cùng nhau.
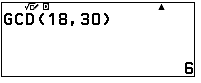
Ví dụ 1: Tìm ước chung lớn nhất của $18$ và $30$.
Bước 1: Phân tích số $18$ và $30$ ra thừa số nguyên tố
$18=2.3^2$
$30=2.3.5$
Bước 2: Thừa số nguyên tố chung là $2$ và $3$
Bước 3: ƯCLN$(18,30)=2.3=6$
Sử dụng máy tính Fx-880btg để kiểm tra đáp án
2. Cách tìm bội chung nhỏ nhất – BCNN.
Muốn tìm BCNN của hai hay nhiều số lơn hơn $1$, ta thực hiện $3$ bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số nguyên tố chung và thừa số nguyên tố riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
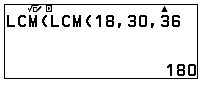
Ví dụ 2: Tìm bội chung nhỏ nhất của $18$, $30$, $36$.
Bước 1: Phân tích các số ra thừa số nguyên tố.
$18=2.3^2$
$30=2.3.5$
$36=2^2.3^2$
Bước 2: Thừa số nguyên tố chung là $2$ và $3$. Thừa số nguyên tố riêng là $5$
Bước 3: BCNN$(18,30,36)=2^2.3^2.5=180$
Sử dụng máy tính Casio Fx-$880$BTG kiểm tra lại kết quả.
Kết Luận: Bài viết giúp các bạn học sinh tiếp cận và nắm được những chức năng cơ bản của máy tính Fx-880 BTG trong bài toán đi tìm ước chung lớn nhất và bội chung nhỏ nhất, giúp việc làm bài tập và kiểm tra đáp án trở nên đơn giản và dễ hiểu hơn.
About Toanbitexdtgd1
