TÌM NGHIỆM NGUYÊN CỦA PHƯƠNG TRÌNH BẬC HAI THEO HAI BIẾN

Ta lấy ví dụ trong câu 6 đề thi chọn đội tuyển TP HCM năm học 2015-2016.

Tìm tất cả các cặp số nguyên dương $x, y$ thỏa phương trình $$x^2+2y=y^2+8x+874$$ 

Gợi ý:

Phương trình có thể được viết: $$(y-1)^2=(x-4)^2-889$$

Do đó điều kiện cho $x>0$ là $x \geqslant 4+\sqrt{889}\approx 33.81610303$.

Xét hàm số $y=1+\sqrt{(x-4)^2-889}$

• Cài đặt chế độ bảng một hàm số để tận dụng 45 giá trị.
• Bấm Menu 8 nhập hàm số
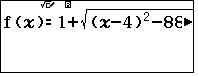
• Phạm vi
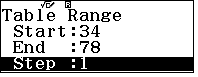
• Duyệt bảng giá trị tìm nghiệm $y$ nguyên

Tương tự xét hàm số $y=1-\sqrt{(x-4)^2-889}$

ta có nghiệm $y$ nguyên   (loại vì $y>0$).

Vậy nghiệm cần tìm là $\left\{\begin{array}{l}x=71\\ y=61\end{array}\right.$.