BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Phần 3: GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ BẰNG MÁY TÍNH CASIO FX-580VNX TRONG CHƯƠNG TRÌNH TRUNG HỌC CƠ SỞ
- 30/12/2018
- 1,034 lượt xem
Toán thực tế là một nội dung khá mới mẻ được đề xuất xuất hiện trong đề thi tuyển sinh môn Toán lớp 10 theo xu hướng ứng dụng những kiến thức được học vào đời sống. Do vậy việc ôn luyện chủ đề này luôn cần phải được quan tâm, nhất là khi các câu hỏi về toán thực tế luôn ở mức độ vận dụng. Đây là loạt bài viết về dạng toán thực tế để học sinh có thể tìm hiểu và giải những dạng toán này dễ dàng hơn. Ở phần 3 này tôi đưa ra hướng dẫn giải một số bài toán thực tế về tính các bài toán diện tích ở thcs.
Phần 3: Giải quyết một số bài toán thực tế về diện tích
Toán thực tế là một nội dung khá mới mẻ được đề xuất xuất hiện trong đề thi tuyển sinh môn Toán lớp 10 theo xu hướng ứng dụng những kiến thức được học vào đời sống. Do vậy việc ôn luyện chủ đề này luôn cần phải được quan tâm, nhất là khi các câu hỏi về toán thực tế luôn ở mức độ vận dụng. Đây là loạt bài viết về dạng toán thực tế để học sinh có thể tìm hiểu và giải những dạng toán này dễ dàng hơn. Ở phần 3 này tôi đưa ra hướng dẫn giải một số bài toán thực tế về tính các bài toán diện tích ở thcs.
Lưu ý: Trong loạt bài viết này chỉ đưa ra hướng dẫn, không phải lời giải. Các em học sinh không nên trình bày theo, rất dễ bị sót điểm trong kiểm tra.
3. Giải quyết một số bài toán thực tế về diện tích
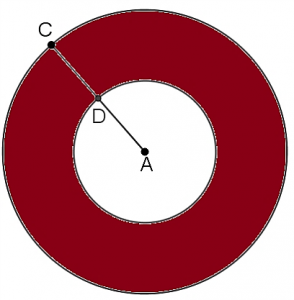
Bài toán thực tế 1: Vòng đệm là một trong những chi tiết lót không thể thiếu giữa đai ốc và các thiết bị ghép nối trong các máy móc công nghiệp. Vòng đệm có tác dụng phân bố đều lực ép lên đai ốc, làm tăng độ chặt giữa các mối ghép. Một vòng đệm có thiết kế như hình vẽ bên, với $latex A$ là tâm của hai đường tròn bán kính $latex AD$ và $latex AC$. Biết $latex D$ là trung điểm của $latex AC$ và $latex AD=r$.
a) Tính diện tích của hình tròn $latex \left( A,AD \right)$ và diện tích của hình tròn $latex \left( A,AC \right)$ theo $latex \pi $ và $latex r$.
b) Tính tỉ số giữa diện tích của miền tô đậm và diện tích của hình tròn $latex \left( A,AC \right)$ .
Hướng dẫn
a) Diện tích của hình tròn $latex \left( A,AD \right)$:
$latex {{S}_{1}}=\pi .{{r}^{2}}$(đvdt)
Diện tích của hình tròn $latex \left( A,AC \right)$:
$latex {{S}_{2}}=\pi .{{\left( 2r \right)}^{2}}=4\pi {{r}^{2}}$(đvdt)
b) Tỉ số giữa diện tích của miền tô đậm và diện tích của hình tròn $latex \left( A,AC \right)$:
$latex \dfrac{4\pi .{{r}^{2}}-\pi .{{r}^{2}}}{4\pi .{{r}^{2}}}=\dfrac{3\pi {{r}^{2}}}{4\pi {{r}^{2}}}=\dfrac{3}{4}$
Bài toán thực tế 2: Một nhóm bạn thân cùng nhau mua bánh kem tổ chức sinh nhật cho bạn Lan. Chiếc bánh kem hình tròn có chu vi bằng $latex 60cm$, bạn Lan cắt ra chia đều cho 6 bạn cùng ăn (mỗi phần bánh là bằng nhau). Tính diện tích phần mặt bánh của một bạn đã ăn?
Hướng dẫn
Bán kính của bánh kem:
$latex C=2\pi \text{R}\Rightarrow R=\dfrac{C}{2\pi }=\dfrac{60}{2\pi }=\dfrac{30}{\pi }\left( cm \right)$
Diện tích phần mặt cái bánh kem:
$latex S=\pi {{\text{R}}^{2}}=\pi {{\left( \dfrac{30}{\pi } \right)}^{2}}=\dfrac{900}{\pi }\left( c{{m}^{2}} \right)$
Diện tích phần mặt bánh một người ăn:
$latex \dfrac{900}{\pi }:6=\dfrac{150}{\pi }\left( c{{m}^{2}} \right)$
Bài toán thực tế 3: Chân một đống cát đổ trên nền phẳng nằm ngang là một hình tròn có chu vi là $latex 10m$. Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông? (làm tròn đến hai chữ số thập phân sau dấu phẩy, biết $latex \pi \approx 3,14$)
Hướng dẫn
Ta có: $latex C=2\pi R=10\Rightarrow R=\dfrac{10}{2\pi }=\dfrac{5}{\pi }\left( cm \right)$
Mà $latex S=\pi {{R}^{2}}=\pi {{\left( \dfrac{5}{\pi } \right)}^{2}}=\dfrac{25}{\pi }\approx 7,96\left( {{m}^{2}} \right)$
Bài toán thực tế 4: Một căn phòng dài $latex 4,2m$, rộng $latex 3,5m$ và cao $latex 3,0m$. Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là $latex 5,4m2$. Hãy tính diện tích cần quét vôi.
Hướng dẫn
Diện tích trần nhà: $latex 4,2.3,5=14,7\left( {{m}^{2}} \right)$
Diện tích bốn bức tường: $latex \left( 4,2.3,0+3,5.3,0 \right).2=46,2\left( {{m}^{2}} \right)$
Diện tích cần quyết: $latex 46,2+14,7-5,4=55,5\left( {{m}^{2}} \right)$
bài toán thực tế 5: Bạn Nam có hai mảnh đất: Một hình vuông và một hình tam giác có kích thước như hình vẽ. Bạn dự định trồng các loại rau quả trên cả hai miếng đất. Hỏi tổng diện tích cả hai miếng đất mà bạn đang có là bao nhiêu?(đơn vị: mét)
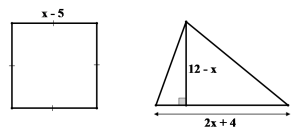
Hướng dẫn
Gọi diện tích của mảnh đất hình vuông là $latex {{S}_{v}}$; diện tích của mảnh đất hình tam giác là $latex {{S}_{tg}}$.
Tổng diện tích mà bạn Nam đang có là $latex S={{S}_{v}}+{{S}_{tg}}={{\left( x-5 \right)}^{2}}+\dfrac{1}{2}\left( 2x+4 \right)\left( 12-x \right)$
$latex \begin{align}& ={{x}^{2}}-10x+25+\left( x+2 \right)\left( 12-x \right) \\& ={{x}^{2}}-10x+25+12x-{{x}^{2}}-2x+24 \\& =25+24=49 \\\end{align}$
Bài toán thực tế 6: Rừng ngập mặn Cần Giờ (còn gọi là Rừng Sác), trong chiến tranh bom đạn và chất độc hóa học đã làm nơi đây trở thành “vùng đất chết” ; được trồng lại từ năm 1979, nay đã trở thành “lá phổi xanh” cho Thành phố Hồ Chí Minh, được UNESCO công nhận là Khu dự trữ sinh quyên của thế giới đầu tiên ở Việt Nam vào ngày 21/01/2000. Diện tích rừng phủ xanh được cho bởi hàm số
$latex S=3,14+0,05t$
trong đó $latex S$ tính bằng nghìn héc-ta, $latex t$ tính bằng số năm kể từ năm 2000. Hãy tính điện tích Rừng Sác được phủ xanh vào các năm 2000 và 2018.
Hướng dẫn
Diện tích Rừng Sác được phủ xanh vào năm 2000
$latex S=3,14+0.05\left( 2000-2000 \right)=3,14$(nghìn héc-ta)
Diện tích Rừng Sác được phủ xanh vào năm 2018
$latex S=3,14+0.05\left( 2018-2000 \right)=4,04$(nghìn héc-ta)
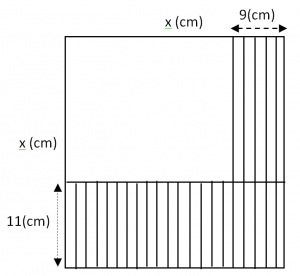
Bài toán thực tế 7: Lập công thức tính diện tích theo $latex x$ phần hình gạch sọc như hình vẽ
Hướng dẫn
Gọi $latex S,{{S}_{x}},{{S}_{t}}$ lần lượt là phần diện tích cần tính, phần diện tích không bị gạch, phần diện tích tổng. Ta có:
$latex \begin{align} & {{S}_{x}}={{x}^{2}}\left( cm \right) \\ & {{S}_{t}}=\left( x+11 \right)\left( x+9 \right)={{x}^{2}}+20x+99\left( cm \right) \\\end{align}$
Vậy diện tích cần tìm
$latex S={{S}_{t}}-{{S}_{x}}={{x}^{2}}+20x+99-{{x}^{2}}=20x+99\left( cm \right)$
———————————————–
Trên đây là một số bài toán thực tế về diện tích ở thcs mà ad sưu tầm được, các bạn có thắc mắc gì về dạng toán thực tế nào thì đừng ngại nhắn tin qua fanpage cho ad nhá, ad sẽ nhiệt tình giải đáp. Trân trọng cám ơn.
About Bitex Khánh Vũ
