BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ÔN TẬP TUYỂN SINH 10- CÁC BÀI TOÁN HÌNH HỌC THƯỜNG GẶP TRONG CÁC KỲ THI TUYỂN SINH LỚP 10 (PHẦN 2)
- 02/05/2019
- 1,140 lượt xem
Tiếp tục bài viết CÁC BÀI TOÁN HÌNH HỌC THƯỜNG GẶP TRONG CÁC KỲ THI TUYỂN SINH LỚP 10, trong bài viết này chúng tôi sẽ tiếp tục gửi đến bạn đọc một vài bài toán hình học với những câu hỏi thường gặp trong các kì thi tuyển sinh lớp 10.
Bài toán 3. Cho nửa đường tròn tâm $O$ đường kính $AB$. Từ điểm $M$ trên tiếp tuyến $Ax$ của nửa đường tròn vẽ tiếp tuyến thứ hai $MC$ ($C$ là tiếp điểm). Hạ $CH$ vuông góc với $AB$, đường thẳng $MB$ cắt nửa đường tròn$\left( O \right)$ tại $Q$ và cắt $CH$ tại $N$. Gọi giao điểm của $MO$ và $AC$ tại $I$. Chứng minh rằng
- Tứ giác $AMQI$ nội tiếp
- $\widehat{AQI}=\widehat{ACO}$
- $CN=NH$
Hướng dẫn giải
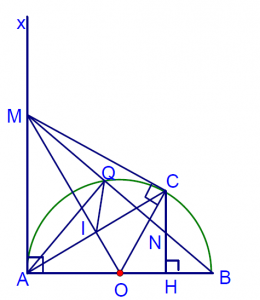
a. Chứng minh tứ giác $AMQI$ nội tiếp
Ta có
$MA,MC$ là hai tiếp tuyến của đường tròn $\left( O \right)$ cắt nhau tại $M$$\Rightarrow MA=MC$
$OA,OB$là bán kính đường tròn $\left( O \right)$ $\Rightarrow OA=OC$
Như vậy ta có: $MO\bot AC\Rightarrow \widehat{MIA}={{90}^{0}}$
$\widehat{AQB}={{90}^{0}}$ (góc nội tiếp chắn nửa đường tròn $\left( O \right)$)
$\Rightarrow \widehat{MQA}={{90}^{0}}$
Hai đỉnh $I$ và $Q$ cùng nhìn $AM$ dưới một góc vuông
Suy ra $AMQI$ là tứ giác nội tiếp
b. Chứng minh $\widehat{AQI}=\widehat{ACO}$
Ta có:
- $AMQI$ là tứ giác nội tiếp nên $\widehat{AQI}=\widehat{AMI}$ (cùng phụ với $\widehat{MAC}$ )
- $\Delta AOC$ cân tại $O$ (do $OA=OC$ ) nên $\widehat{CAO}=\widehat{ACO}$
- $\widehat{AMI}=\widehat{CAO}$
Suy ra $\widehat{AQI}=\widehat{ACO}$
c. Chứng minh $CN=NH$
Gọi $K$ là giao điểm của $BC$ và tia $Ax$
Ta có $\widehat{ACB}={{90}^{0}}$ (góc nội tiếp chắn nửa đường tròn $\left( O \right)$)
$AC\bot BK$, $AC\bot OM\Rightarrow BK//OM$
Xét $\Delta ABK$ ta có: $OA=OB,OM//BK$
$\Rightarrow MA=MK$
Áp dụng hệ quả của định lý Talet vào $\Delta BKM$ với $NH//AM$ ta có: $\dfrac{NH}{AM}=\dfrac{BN}{BM}$ (1)
Áp dụng hệ quả của định lý Talet vào $\Delta BKM$ với $CN//KM$ ta có: $\dfrac{BN}{BM}=\dfrac{CN}{KM}$ (2)
Từ (1) và (2) suy ra $\dfrac{NH}{AM}=\dfrac{CN}{KM}$
Mà $AM=KM$ nên $NH=CN$ (đpcm)
Bài toán 4. Cho $\Delta ABC$ có ba góc nhọn. Đường tròn đường kính $BC$ cắt cạnh $AB,AC$ lần lượt tại $E,F$ ; BF cắt $EC$ tại $H$. Tia $AH$ cắt đường thẳng $BC$ tại $N$
- Chứng minh $HFCN$ là tứ giác nội tiếp
- Chứng minh $FB$ là phân giác của $\widehat{EFN}$
- Giả sử $AH=BC$. Tính số đo của $\widehat{BAC}$
Hướng dẫn giải
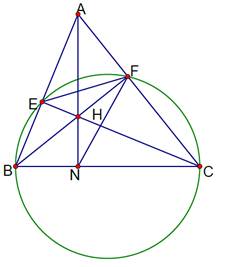
a. Chứng minh $HFCN$ là tứ giác nội tiếp
Ta có $E,F$ thuộc đường tròn có đường kính $BC$ $\Rightarrow \widehat{BFC}=\widehat{BEC}={{90}^{0}}$
Xét tứ giác $HFCN$ ta có $\widehat{HNC}+\widehat{HFC}={{180}^{0}}$
Vậy $HFCN$ là tứ giác nội tiếp đường tròn đường kính $HC$
b. Chứng minh $FB$ là phân giác của $\widehat{EFN}$
Xét đường tròn đường kính $BC$ ta có $\widehat{EFB}=\widehat{ECB}$ (góc nội tiếp cùng chắn cung $\overset\frown{EB}$ )
Xét đường tròn đường kính $HC$ ta có $\widehat{HFN}=\widehat{HCN}$ (góc nội tiếp cùng chắn cung $\overset\frown{HN}$)
Mà $\widehat{ECB}\equiv \widehat{HCN}$ nên $\widehat{EFB}=\widehat{HFN}$
Suy ra $FB$ là phân giác của $\widehat{EFN}$
c. Giả sử $AH=BC$. Tính số đo của $\widehat{BAC}$
Xét $\Delta FAH$vuông tại $F$ và $\Delta FBC$ vuông tại $F$ ta có:
- $AH=BC$ (gt)
- $\widehat{FAH}=\widehat{FBC}$ (cùng phụ với $\widehat{BCA}$ )
Vậy $\Delta FAH=\Delta FBC$ $\Rightarrow FA=FB$
Suy ra $\Delta FAB$ vuông cân tại $F$
$\Rightarrow \widehat{BAC}=\widehat{BAF}={{45}^{0}}$
Bài toán 5. Cho $\Delta ABC$ vuông tại $A$, đường cao $AH$. Đường tròn tâm $O$ đường kính $AH$cắt cạnh $AB,AC$ tại $M,N$ ($M,N\ne A$ ). Gọi $I,P,Q$ lần lượt là trung điểm của của $OH,BH,CH$.
Chứng minh
- $\widehat{AHN}=\widehat{ACB}$
- Tứ giác $BMNC$ nội tiếp
- $I$ là trực tâm của $\Delta APQ$
Hướng dẫn giải
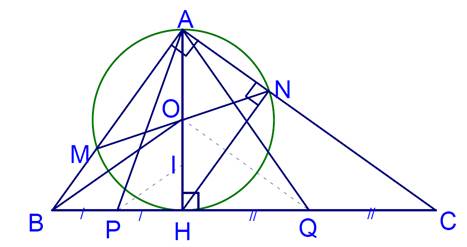
a. Chứng minh $\widehat{AHN}=\widehat{ACB}$
Xét $\Delta AHC$ vuông tại $H$ ta có $\widehat{HAC}+\widehat{ACB}={{90}^{0}}$(1)
Ta có $N$ thuộc đường tròn đường kính $AH$
$\Rightarrow \Delta NAH$ vuông tại $N$ $\Rightarrow \widehat{HAN}+\widehat{AHN}={{90}^{0}}$ (2)
Từ (1) và (2) suy ra $\widehat{ACB}=\widehat{AHN}$ (do $\widehat{HAC}\equiv \widehat{HAN}$ )(đpcm)
b. Chứng minh tứ giác $BMNC$ nội tiếp
Ta có:
- $\widehat{ACB}=\widehat{AHN}$(cmt)
- $\widehat{AMN}=\widehat{AHN}$ (góc nội tiếp cùng chắn cung $\overset\frown{AN}$ )
$\Rightarrow \widehat{ACB}=\widehat{AMN}$
Ta có $\widehat{AMN}+\widehat{NMB}={{180}^{0}}$ (do $A,M,B$thẳng hàng)
$\Rightarrow \widehat{ACB}+\widehat{NMB}={{180}^{0}}$ hay $\widehat{NCB}+\widehat{NMB}={{180}^{0}}$
Suy ra tứ giác $BMNC$ nội tiếp (đpcm)
c. Chứng minh $I$ là trực tâm của $\Delta APQ$
Xét $\Delta AHC$ ta có:
- $OH=OA$ (do $AH$ là đường kính của đường tròn tâm $O$ )
- $QH=QC$ (do $Q$ là trung điểm của $HC$ )
Suy ra $QO$ là đường trung bình của $\Delta AHC$ $\Rightarrow QO//AC$
Mà $AB\bot AC$ nên $AB\bot QO$
Xét $\Delta OBH$ ta có $I,P$ lần lượt là trung điểm của $OH,BH$
Suy ra $IP$ là đường trung bình của $\Delta OBH$$\Rightarrow IP//OB$ (3)
Xét $\Delta ABQ$ ta có $QO\bot AB$ và $AO\bot BQ$, suy ra $O$ là trực tâm của $\Delta ABQ$
$\Rightarrow BO\bot AQ$ (4)
Từ (3) và (4) suy ra $IP\bot AQ$
Mặt khác ta có $AI\bot PQ$ (gt)
Như vậy $I$ là trực tâm $\Delta APQ$ (đpcm)
Cảm ơn các bạn đã theo dõi bài viết CÁC BÀI TOÁN HÌNH HỌC THƯỜNG GẶP TRONG CÁC KỲ THI TUYỂN SINH LỚP 10 (PHẦN 2). Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
