BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Một bài toán 3 điểm thẳng hàng phải dùng đến nhiều tứ giác nội tiếp
- 17/02/2023
- 211 lượt xem
| Việc chứng minh 3 điểm thẳng hàng là một công việc quen thuộc ở lớp 7-8. Tuy nhiên trong một số bài toán hình học lớp 9, việc đó có vẻ không dễ dàng, như ví dụ dưới đây: |
| Từ một điểm $M$ nằm ngoài $(O)$ vẽ hai tiếp tuyến $MA, MB$ và cát tuyến $MCD$ với $(O)$ ($A,B$ là tiếp điểm và cát tuyến $MCD$ nằm trong $\widehat{AMO}$ với $MC < MD$). Tiếp tuyến tại $C$ của $(O)$ cắt $MB$ tại $E$. Gọi $I$ là hình chiếu vuông góc của $E$ lên đường thẳng $MO$. Chứng minh ba điểm $A, C, I$ thẳng hàng. |
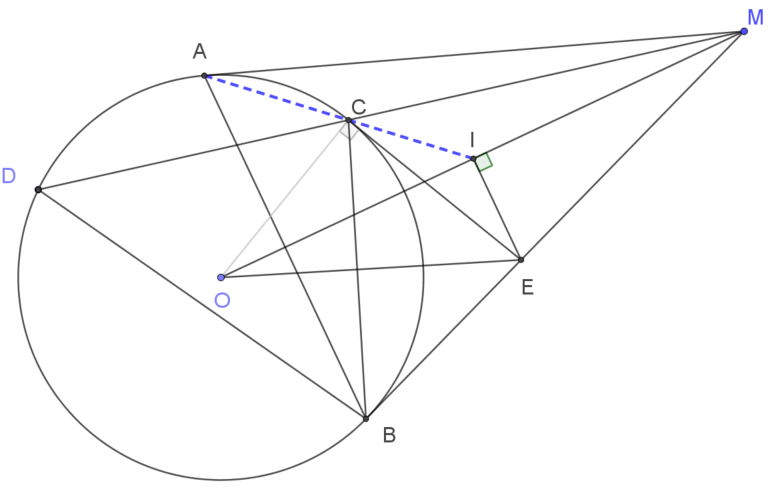
Gợi ý: Ta chỉ cần chứng minh $\widehat{ACO}+\widehat{ECI}=90^\circ$.
– $\widehat{ECI}=\widehat{EOI}$ (tứ giác $COEI$ nội tiếp đường tròn đường kính $OI$.)
– $\widehat{ACO}=\widehat{OAC}=\widehat{OAB}+\widehat{BAC}$
Lưu ý $\left\{\begin{array}{l}\widehat{OAB}=\widehat{OMB} \quad \text{(tứ giác}\ MAOB\ \text{nội tiếp đường tròn đường kính} MO.)\\
\widehat{BAC}=\widehat{MBC}\quad \text{(cùng chắn cung}\ BC)\end{array}\right.$
Suy ra $\widehat{ACO}= \widehat{MBC}+\widehat{OMB}=\widehat{OEI}$ (các bạn tự kiểm tra dựa vào các tam giác vuông liên quan với chú ý $BC\perp OE$ do $OE$ là đường trung trực của $BC$).
Vậy $\widehat{ACO}+\widehat{ECI}=\widehat{OEI}+\widehat{EOI}=90^\circ$ (đpcm).
Một học sinh lớp 9 đã trình bày lời giải sau đây:
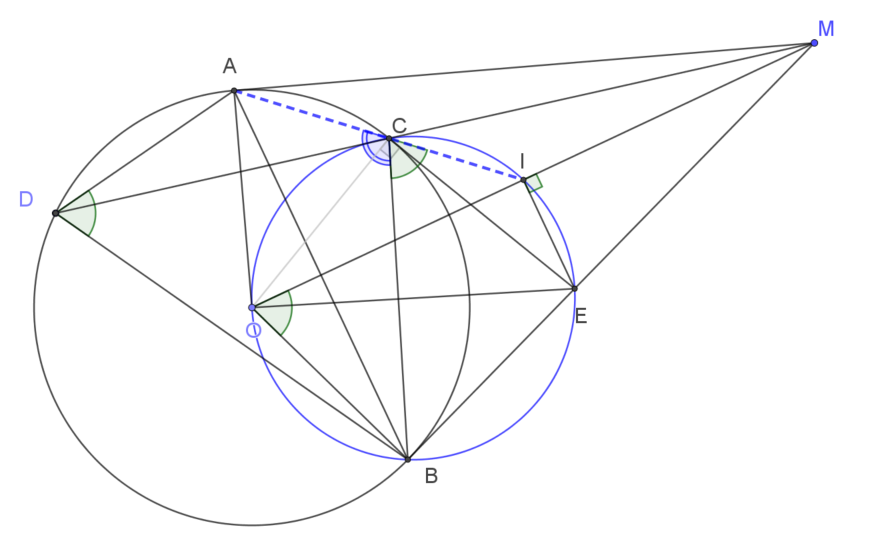
| năm điểm $O, E, C, I, B$ nằm trên đường tròn đường kính $OE$.
Vậy $\widehat{ICB}=\widehat{IOB}\quad (1)$ Do $OM$ là tia phân giác của góc $\widehat{AOB}$ nên $\widehat{IOB}=\dfrac12\widehat{AOB}\quad (2)$ Góc $\widehat{ADB}$ là góc nội tiếp và góc $\widehat{AOB}$ là góc ở tâm cùng chắn cung $AB$ nên: $\dfrac12\widehat{AOB}=\widehat{ADB}\quad (3)$. Từ $(1), (2)$ và $(3)$ ta suy ra: $\widehat{ICB}=\widehat{ADB}$. Vậy $$\widehat{ICA}=\widehat{ICB}+\widehat{ACB}=\widehat{ADB}+\widehat{ACB}=180^\circ \quad \text{do tứ giác} \ ADBC \ \text{nội tiếp}.$$ |
About TS. Nguyễn Thái Sơn
