XÂY DỰNG MỘT SỐ HỆ THỨC LƯỢNG TRONG TAM GIÁC
- 21/12/2021
- 941 lượt xem
Trong kỳ thi học sinh giỏi máy tính cầm tay cấp thành phố, đặc biệt là thành phố Hồ Chí Minh, thí sinh phải giải một tam giác khi biết ba cạnh. Trong khuôn khổ lớp 10, vấn đề này được trình bày trong giáo khoa. Ở đây trong khuôn khổ lớp 9 và yêu cầu cần thiết cho kỳ thi học sinh giỏi máy tính, chúng tôi xây dựng các hệ thức lượng này. Các GV phụ trách dội tuyển chứng minh công thức cho học sinh (như sinh hoạt ngoại khoá), riêng học sinh thì thuộc công thức để sử dụng.
- Hệ thức trung tuyến.
Trong một tam giác tổng bình phương hai cạnh bằng hai lần bình phương trung tuyến ứng với cạnh thứ ba cộng với nửa bình phương của cạnh thứ ba.
Chứng minh. Giả sử $AB<AC$, các trường hợp còn lại chứng minh tương tự.

Ta có
$AB^2=AH^2+BH^2$
$AC^2=AH^2+HC^2$
Suy ra $AB^2+AC^2=2AH^2+BH^2+HC^2=2(AM^2-HM^2)+BH^2+HC^2$
Ta tính riêng $BH^2+BC^2-2HM^2$ với
$HM=BM-BH =\dfrac{BC}{2}-BH=\dfrac{BH+CH}{2}-BH=\dfrac{CH-BH}{2}$
$ \Rightarrow HM^2=\dfrac{BH^2+CH^2-2BH.CH}{4}$.
Do đó $BH^2+BC^2-2HM^2=\dfrac{BH^2+CH^2+2BH.CH}{2}=\dfrac{(BH +CH)^2}{2}=\dfrac{BC^2}{2}$.
Tóm lại $AB^2+AC^2=2AM^2+\dfrac{BC^2}{2}$
Áp dụng: Cho tam giác $ABC$ có cạnh $AB = 5,7; BC = 8,3; CA = 7,6$. Đường trung tuyến $AM$ cắt phân giác $BD$ tại $I$. Tính (chính xác đến 2 chữ số thập phân): các đoạn $IA, IB, IC$.
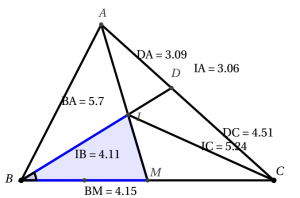
Áp dụng hệ thức trung tuyến, ta có:
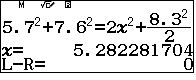

Theo tính chất của đường phân giác trong ta có:
$$\dfrac{IA}{IM}=\dfrac{BA}{BM} \Leftrightarrow BM.IA=BA.IM$$


Vậy $IA=3,06$
- Tính các góc trong tam giác.
Trong một tam giác bình phương của một cạnh bằng tổng bình phương hai cạnh còn lại trừ hai lần tích của hai cạnh đó nhân với cosin của góc tạo bởi hai cạnh đó.
Chứng minh.
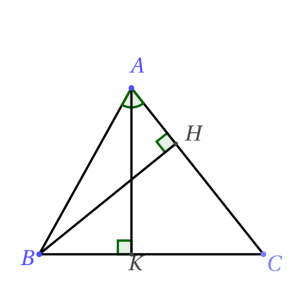
Ta chỉ xét tam giác nhọn.$BC^2=(BK+KC)^2=BK^2+KC^2+2.BK.CK$
$=AB^2-AK^2+AC^2-AK^2+2.BK.CK$
$=AB^2+AC^2-2(AK^2-BK.CK)$
Ta lại có: $CH.CA=CK.CB \Leftrightarrow (AC-AH)AC=CK(CK+KB)$
$\Leftrightarrow AC^2-CK^2-CK.KB=AH.AC$
mà $AH=AB.\cos A$ nên $AH.AC=AB.AC\cos A$.
Tóm lại:
$BC^2=AB^2+AC^2-2AB.AC\cos A$
Áp dụng. Tính IB, IC
Ta có: $\cos B=\dfrac{BA^2+BC^2-AC^2}{2.BA.BC}=$
 $\Rightarrow \widehat{B}=$
$\Rightarrow \widehat{B}=$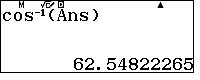 $\Rightarrow \dfrac{\widehat{B}}{2}=$
$\Rightarrow \dfrac{\widehat{B}}{2}=$ $\cos\dfrac{\widehat{B}}{2}=$
$\cos\dfrac{\widehat{B}}{2}=$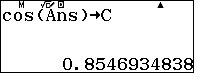
Trong tam giác $ABI$ ta có:
$$IA^2=BA^2+BI^2-2BA.BI\cos\dfrac{\widehat{B}}{2}$$
$$x^2-2xBA\cos\dfrac{\widehat{B}}{2}+BA^2-IA^2=0$$
Bấm ![]() nhập hệ số
nhập hệ số
$a=1 , b=-2\times 5.7\times C, c=5.7^2-B^2 $ với $B$ và $C$ là hai biến nhớ đã lưu, lưu ý không làm tròn số trong quá trình tính ra đáp số cuối cùng.

Ta nhận nghiệm $x_2$ 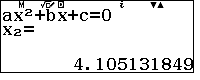
Vậy $IB=4,11$ lưu vào D.
Trong tam giác $IBC$ ta có: $IC^2=BI^2+BC^2-2.BI.BC.\cos \dfrac{\widehat{B}}{2}$
Vậy $IC=5,24  $
$
TÓM TẮT GIÁO KHOA
1. Hệ thức trung tuyến:
$$AB^2+AC^2=2AM^2+\dfrac{BC^2}{2}$$
2. Tính ba góc:
$$BC^2=AB^2+AC^2-2AB.AC\cos A$$
$$\Rightarrow \cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}$$
3. Chiều dài đường phân giác trong
Các em học sinh ghi nhận công thức sau đây. Các GV có thể chứng minh cho các em trong buổi sinh hoạt ngoại khoá. Mục đích của việc ghi nhớ công thức này là để giải nhanh bài thi học sinh giỏi máy tính cầm tay cấp thành phố.
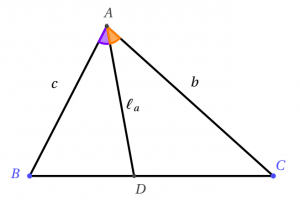
$$\ell =\dfrac{2bc}{b+c}\cos \dfrac{A}{2}$$
$\ell$ là độ dài đường phân giác trong kẻ từ đỉnh $A$, $b=AC, c=AB$.
Áp dụng tính trực tiếp IB trong bài toán trên:
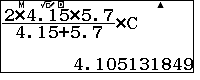
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay