BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm số N có 14 chữ số thỏa mãn điều kiện đồng dư
- 24/10/2017
- 536 lượt xem
Tìm số [latex]N[/latex] có 14 chữ số, biết rằng $N$ chia 7741 dư 2017, chia 2017 dư 2013, chia 2013 dư 2011.
Bài giải
Vì các số [latex]7741,\,2017,\,2013[/latex] đôi một nguyên tố cùng nha, nên ta đi giải hệ phương trình đồng dư sau:
$$\begin{cases} x\equiv2017 & \text{mod}\,7741\\ x\equiv2013 & \text{mod}\,2017\\ x\equiv2011 & \text{mod}\,2013 \end{cases}\,\,\,(I)$$
Thì hệ có nghiệm duy nhất theo modulo [latex]M=7741\times 2017\times 2013[/latex] là:
$$x\equiv a_1.M_1.y_1+a_2.M_2.y_2+a_3.M_3.y_3$$
Trong đó [latex]a_1=2017;\,a_2=2013;\,a_3=2011[/latex]; [latex]M_1=2017\times 2013; M_2=7741 \times 2013; M_3=7741 \times 2017[/latex]; [latex]y_1=(M_1)^{-1}\,\,\text{mod}m_1; y_2=(M_2)^{-1}\,\,\text{mod}m_2; y_3=(M_3)^{-1}\,\,\text{mod}m_3[/latex].
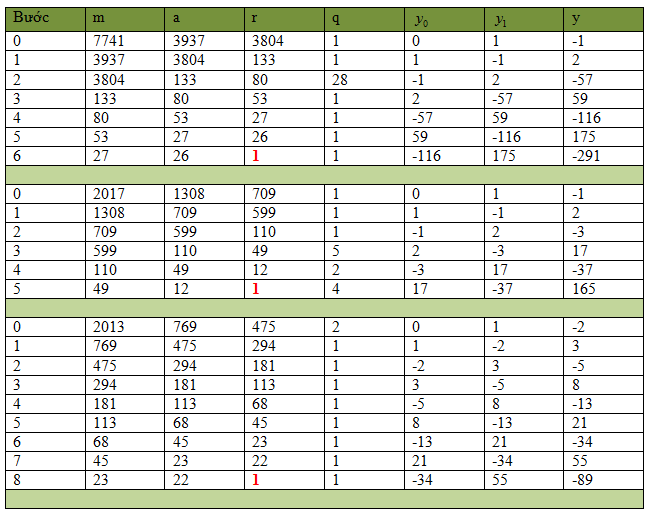
Vấn đề ta đi tìm nghịch đảo bằng cách áp dụng thuật toán Euclid:
+ Tìm nghịch đảo của 3937 theo modulo 7741: 7450.
+ Tìm nghịch đảo 1308 theo modulo 2017: 165.
+ Tìm nghịch đảo 769 theo modulo 2013: 1924.
Vậy nghiệm là: [latex]x=2017\times 2017 \times 2013 \times 7450+2013 \times 7741 \times 2013 \times 165 + 2011 \times 7741 \times 2017 \times 1924 = 12659878950343[/latex].
Nghiệm [latex]x[/latex] cần tìm: [latex]x \equiv 29483295796 + 31430170761a[/latex] và từ đây, dựa theo điều kiện đề bài để tìm số [latex]s[/latex] nguyên cho phù hợp.
Kết luận số cần tìm: 99977426315776.
Xem thêm hình ảnh về quá trình tìm nghịch đảo theo modulo:
About TailieuCasio
