BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tìm dư của phép chia khi số bị chia có dạng $a^n$
- 28/12/2022
- 1,139 lượt xem
| Bài toán: Tìm dư của phép chia số $2024^{2023}$ cho $2022$. |
Ý tưởng: Phân tích số đã cho thành một tích có số hạng tổng quát là $2024^{2^x}$ (số sau là bình phương số trước). Sau đó tìm dư của phép chia mỗi số hạng cho $2022$. Lấy các dư nhân cho nhau rồi chia cho số chia sẽ ra được dư cuối cùng, chính là dư của phép chia đã cho. Vận dụng kết quả sau nghĩa là: $$2024^{2023}=\underbrace{2024^{2^5}\times 2024^{2^6}\times 2024^{2^7}\times 2024^{2^8}\times 2024^{2^9}\times 2024^{2^{10}}}_{\text{số sau là bình phương số trước}}\times \underbrace{2024^{2^2}\times 2024^{2^1}\times 2024^{2^0}}_{\text{tổng các số mũ là 7}}$$ |
$2024^{2^0}$ 
$2024^{2^1}$ 
$2024^{2^2}$ 
không sử dụng $2024^{2^3}, 2024^{2^4}$ nhưng phải nhấn exe: 
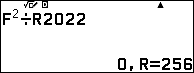
$202^{2^5}$ 
$202^{2^6}$ 
$202^{2^7}$ 
$202^{2^8}$ 
$202^{2^9}$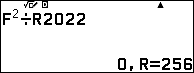 
$202^{2^{10}}$ 
Thực hiện phép chia có dư các cho các dư số đã được thiết lập:
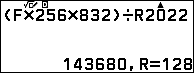
Vậy dư của phép đã cho là số $\Huge\color{blue}{128}$
Chia sẻ
About TS. Nguyễn Thái Sơn
