Tìm 5 chữ số tận cùng của số $a^n$, a là một số nguyên tố và n là số năm (year)

Ta có nhận xét:

Vậy $5^{2016}=\underbrace{5^{2^5}\times 5^{2^6}\times 5^{2^7}\times 5^{2^8}\times 5^{2^9}\times 5^{2^{10}}}_{\text{Số sau là bình phương của số trước}}$.

Ta có: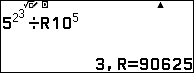

Nhập biểu thức

Nhấn EXE 2 lần ta có $5^{2^5}\equiv $ (R mod $10^5$) với .

Vậy $5^{2016}\equiv (90625\times 90625\times 90625\times 90625\times 90625\times 90625)$ (mod $10^5$)

Suy ra $$5^{2016}\equiv 90625\quad (\text{mod}\ 10^5)$$.

Kết quả tham khảo:

Nhận xét: $7^{2022}=\underbrace{7^{2^5}\times 7^{2^6}\times 7^{2^7}\times 7^{2^8}\times 7^{2^9}\times 7^{2^{10}}}_{\text{sô sau là bình phương số trước }}\times 7^6$.

5 chữ số tận cùng của $7^{2^4}$ là $69601$ 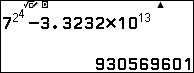lưu vào F.
.

Suy ra 5 chữ số cuối của $7^{2^5}$ là R

Nhấn EXE 5 lần lấy 5 kết quả

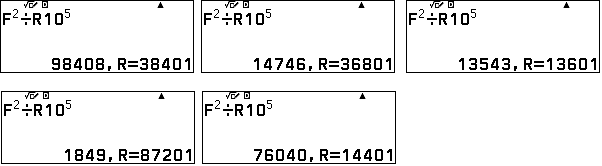
Riêng $7^6$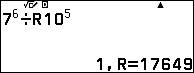

Vậy $7^{2022} \equiv (99201\times 38401\times 36801\times 13601 \times 87201\times 14401\times 17649) $ (mod $10^5$).

Nhân 4 số đầu tiên với nhau lấy 5 chữ số cuối cùng của kết quả

Nhân 3 số cuối cùng với nhau lấy 5 chữ số cuối cùng của kết quả

Và sau đây là kết quả 5 chữ số cuối cùng cần tìm của $7^{2022}$ là $88049$

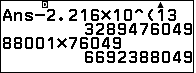
Kết quả tham khảo:

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013).