BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Thuật toán tìm nghịch đảo mô-đu-lô trên MTCT
- 29/11/2021
- 6,436 lượt xem
Trong định lý phần dư Trung Hoa với các số đưa vào khá lớn, ta không dùng chức năng lập bảng mà phải dùng nghịch đảo của một số theo mô-đu-lô.
Ta quy định các số trong bài này là các sô tự nhiên.
| Đinh nghĩa: Số $z$ được gọi là nghich đảo của số $y$ theo mô-đu-lô $A$ nếu $yz\equiv 1\ \text{mod}\ A$. |
Thuật toán trên máy tính Casio fx-580VN X như sau:
|
A$\div$Ry:z=C-DE:A=y:y=F:C=D:D=z
|
Ví dụ: Tìm nghịch đảo của 3937 theo modulo 7741.
Trước hết ta lấy $7741$ lưu vào A, $3937$ lưu vào y  Sau đó thực hiện phép chia có dư A cho y trên MTCT  Tiếp theo viết thuật toán lên màn hình, bấm CALC máy tính sẽ hỏi A ta bấm mũi tên xuống (tức là chấp nhận đề nghị), hỏi y ta chấp nhận, hỏi C ta nhập 0, hỏi D ta nhập 1, hỏi E ta chấp nhận, hỏi F ta chấp nhận.Cuối cùng nhấn Enter (=) nhiều lần cho đến khi vào thấy dư R=1 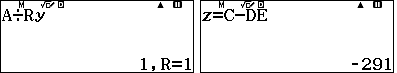 thì dừng lại, nhấn enter (=) sẽ thấy $z$. |
Vậy nghịch đảo của 3937 theo modulo 7741 là $-291$.
Áp dụng – Bài thi HSG MTCT THCS
Xét phương trình đồng dư
$$\left\lbrace\begin{array}{llll}
x & \equiv & 2017 & (\text{mod} \ 7741)& \\
x & \equiv & 2013 & (\text{mod} \ 2017)& \\
x & \equiv & 2011 & (\text{mod} \ 2013)
\end{array} \right.
$$
Nghiệm của hệ phương trình đồng dư là
$$x=a_1y_1z_1+a_2y_2z_2+a_3y_3z_3+(7741\times 2017\times 2013)k$$
trong đó
$a_1=2017, y_1=2017\times 2013$
$a_2=2013, y_2=7741\times 2013$ 
$a_3=2011, y_3=7741\times 2017$ 
Tìm các nghịch đảo mô-đu-lô như trên cho $1308$ và $769$ ta có $z_2=163$ và $z_3=-89$
$$x \equiv a_1y_1z_1+a_2y_2z_2+a_3y_3z_3 + k n_1n_2n_3 \equiv 126598780950343+31430170761k, k \in \mathbb{Z}$$
Để $x$ lớn nhất có 14 chữ số, số nguyên $k$ lớn nhất thoả điều kiện $k \leqslant\ $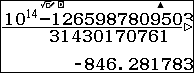 
. Vậy $k=-847$
Vậy số cần tìm là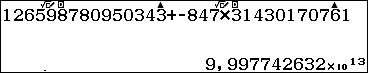 
$= 99.977.426.315.776$
About TS. Nguyễn Thái Sơn
