BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng Phương pháp tọa độ giải bài thi HSG Casio 2022
- 21/11/2022
- 1,006 lượt xem
Đây là bài thi thuộc khối THCS. Vì chúng ta đã biết phương trình đường thẳng, giao điểm của hai đường thẳng v.v… Bây giờ chúng ta chỉ tìm hiểu cách chuyển từ tọa độ cực sang tọa độ thông thường.
| Trong mặt phẳng $Oxy$ nếu một điểm $M$ cách gốc tọa độ $O$ một đoạn $r$ và hợp với trục hoành một góc $a$ (dương hoặc âm) thì tọa độ của điểm $M$ là $M(r\cos a, r\sin a)$. Trên máy tính casio fx-880BTG chúng ta sử sử dụng |
CATALOG 
.
|
Cú pháp
|
Sau khi chuyển sang tọa độ thông thường. máy tính sẽ tự động lưu vào $x, y$.
GIẢI BÀI TOÁN
a)
Ta tìm tọa độ điểm $M$ là giao điểm của hai đường thẳng $BC$ và $AD$.
$AD: y=(\tan 54^\circ) x$
$BC: x+y-9,8=0$
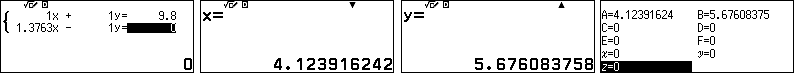
Lưu $x$ và $y$ vào các biến nhớ A và B.
Vậy $AM, BM$ lần lượt là:
b)
Việc tính diện tích tứ giác $AMNP$ được thực hiện như sau:
$$S_{AMNP}=\left(1-\dfrac{CN}{CM}.\dfrac{CP}{CA}\right).S_{CAM}$$
trong đó $CP=AC-AM$.
Tọa độ cực của điểm $D$ là $(9,8;54)$ nên tọa độ thông thường là $(x,y)$ máy tự động lưu vào $x$ và $y$.
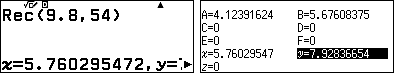
Để tính $CN$ ta tìm tọa độ giao điểm $N$ của $BC$ và $DP$ lưu vào C và D.
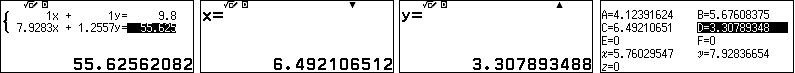
Lập tỉ số (phần ở trong ngoặc đơn của công thức ở trên):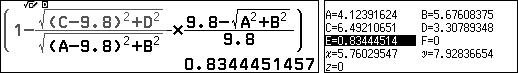 
Vậy $S_{AMNP}=$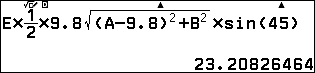 
|
Nhận xét: Việc sử dụng tọa độ giúp việc giải bài toán theo một tuyến đơn giản, không sử dung nhiều hệ thức lượng trong tam giác.
|
About TS. Nguyễn Thái Sơn
