BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GTNN CỦA HÀM SỐ (TIẾP THEO)
- 19/11/2019
- 561 lượt xem
- Kỳ trước ta đã khảo sát hàm số $ y=\dfrac{ax^2+bx+c}{a’x^2+b’x+c’}$ để tìm GTLN và GTNN của hàm số này. Để thực hiện công việc này ta tìm tập hợp giá trị của hàm số, đó là nghiệm của bất phương trình bậc hai theo biến $y$ sau đây:
$$\Delta_m y^2+(4ac’+4a’c-2bb’)y+\Delta_t\geqslant 0$$
trong đó $\Delta_m$ là biệt thức của mẫu và $\Delta_t$ là biệt thức của tử.
Bây giờ nếu yêu cầu của bài toán là chỉ tìm GTNN hoặc GTLN của hàm số ta có thể dùng bảng với 45 giá trị thuộc tập xác định của hàm số.
- Cài đặt máy tính để bảng chỉ làm việc với một hàm số
- Nhập hàm số, phạm vi chọn từ -22 đến 22 hoặc 45 số nguyên thích hợp tùy theo bài toán.
- Duyệt bảng tìm GTNN hoặc GTLN (thô).
- Tinh chỉnh tập xác định để tìm GTNN hoặc GTLN (mịn)
Ví du: Tìm GTNN của hàm số $y=\dfrac{1,2x+5,9}{\sqrt{2,3x-7,4}}$
- Nhập hàm số
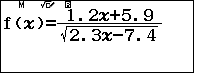
- Phạm vi (thô)
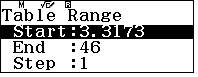
- GTNN (thô)
(GTNN $\approx 4.5134$) - Tinh chỉnh tập xác định
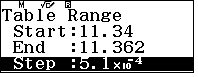
- Định dạng số thập phân với 4 số lẻ sau dấu phẩy, ta thấy GTNN của hàm số là
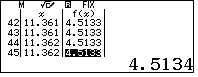(lưu ý f(x) luôn luôn bằng 4.5134 với 45 giá trị thuộc tập xác định của hàm số ). - Vậy GTNN của hàm số (chính xác tới 4 số lẻ thập phân sau dấu phẩy) là $4.5134$
Chia sẻ
About TS. Nguyễn Thái Sơn
