BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Định lý thặng dư Trung Hoa và áp dụng - bài 2
- 22/08/2021
- 1,281 lượt xem
Bài luyện tập – bài thi HSG MTCT THCS
Tìm số tự nhiên $x$ lớn nhất có 14 chữ số, biết $x$ chia cho $7741$ dư $2017$, chia cho $2017$ dư $2013$ và chia cho $2013$ dư $2011$.
Xét phương trình đồng dư
$$\left\lbrace\begin{array}{llll}
x & \equiv & 2017 & (\text{mod} \ 7741)& \\
x & \equiv & 2013 & (\text{mod} \ 2017)& \\
x & \equiv & 2011 & (\text{mod} \ 2013)
\end{array} \right.
$$
Áp dụng thuật toán “nghịch đảo mô-đu-lô” trong bài 1
ta tìm được $z_1, z_2$ và $z_3$ như sau:
- $\bullet\ $
- $\bullet\ $
- $\bullet\ $
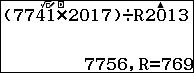
Ta có
$a_1y_1z_1=2017\times 2017\times 2013\times (-291)$
$a_2y_2z_2=2013\times 7741\times 2013\times 165$
$a_3y_3z_3=2011\times 7741\times 2017\times (-89)$
$$x \equiv a_1y_1z_1+a_2y_2z_2+a_3y_3z_3 + k n_1n_2n_3 \equiv 126598780950343+31430170761k, k \in \mathbb{Z}$$
Để $x$ lớn nhất có 14 chữ số, số nguyên $k$ lớn nhất thoả điều kiện $k \leqslant\ $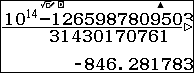 
. Vậy $k=-847$
Vậy số cần tìm là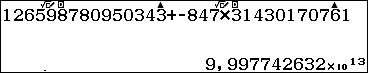 
$99.977.426.315.776$
Chia sẻ
About TS. Nguyễn Thái Sơn
