BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải nhanh bài toán GTLN và GTNN trên MTCT
- 13/12/2021
- 631 lượt xem
| Tìm GTLN và GTNN của hàm số $$y=\dfrac{ax^2+bx+c}{dx^2+ex+f}$$ trong đó $\Delta_m=e^2-4df<0$ |
Tập giá trị của hàm số là nghiệm của bất phương trình $$\Delta_my^2+(4af+4cd-2be)y+\Delta_t\geqslant 0.$$
Áp dụng:
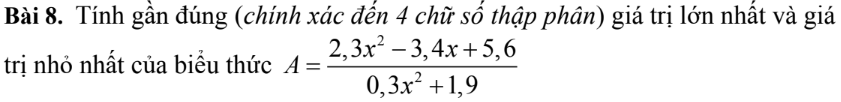
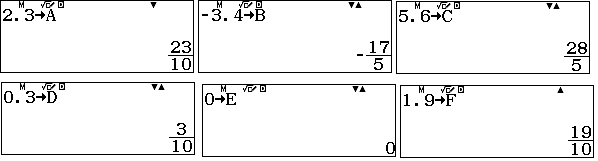
Bấm MENU A 23 để mở bất phương trình $ax^2+bx+c\geqslant 0$ trên máy tính rồi nhập các hệ số, lưu ý các hệ số này rất dễ nhập do vị trí của các biến ABCDEF :
và kết quả là
Chia sẻ
About TS. Nguyễn Thái Sơn
