BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BÀI GIẢI KỲ THI CHỌN ĐỘI TUYỂN TP.HCM NĂM 2015
- 05/11/2019
- 670 lượt xem
Câu 1: Tìm số tự nhiên $x$ nhỏ nhất có 10 chữ số, biết $x$ chia cho 17 có dư là 5, chia cho 29 có dư là 11 và chia cho 43 có dư là 25.
Gợi ý: Các thầy cô dạy đội tuyển có thể có lời giải đặc sắc. Ở đây chúng tôi giới thiệu cách giải đơn giản dành cho các thầy cô mới nhận nhiệm vụ.
Ta có: $x=17k+5=29l+11=43m+25, (k,l,m \in \mathbb{N})$.
Do $x$ có 10 chữ số nên $29l+11 \geqslant 10^9 \Rightarrow l \geqslant 34482759$.
Vì $k=\dfrac{29l+6}{17}$ nên lập bảng cho hàm số $f(x)=\dfrac{29x+6}{17}$
- Cài đặt bảng 1 hàm số để tận dụng 45 giá trị.
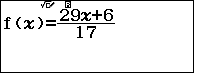
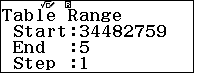
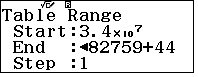
- Khi máy tính xuất ra bảng giá trị, ta duyệt giá trị nguyên đầu tiên của $k$ là
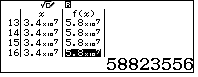
Vì $m=\dfrac{17k-20}{43}$ nên lập bảng cho hàm số $g(x)=\dfrac{17x-20}{43}$ với $x$ nguyên bắt đầu từ $58823556$.
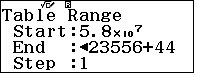
- Khi xuất ra bảng giá trị, ngay tại $x=58823556\Rightarrow f(x)=$
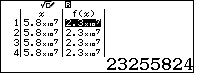nghĩa là $m=23255824 \in \mathbb{N}$.
Vậy số tự nhiên cần tìm là $x=k\times 17+5=$ 
P/S.
- Nếu may mắn thì khi nhận được $k=58823556$ ta đã có $x=17k+5$.
- Nếu không may, giá trị đầu tiên của $m$ nói trên không phải là số nguyên, thì ta ghi nhận các giá trị nguyên $m$ của hàm $g(x)$ rồi thực hiện ngược trở lại cho hàm $h(x)=\dfrac{43x+20}{17}$ để tìm số nguyên $k$ đầu tiên. Từ $k$ đó ta suy ra $x$ tương ứng.
- Để hạn chế rủi ro, khi xuất ra bảng giá trị của hàm số $f(x)=\dfrac{29x+6}{17}$ ta tranh thủ tìm thêm các giá trị nguyên của $k$ ngoài số 58823556.
Chia sẻ
About TS. Nguyễn Thái Sơn
