BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ BẰNG MÁY TÍNH CASIO FX-580VNX TRONG CHƯƠNG TRÌNH TRUNG HỌC CƠ SỞ
- 06/01/2022
- 2,855 lượt xem
Toán thực tế là một nội dung khá mới mẻ được đề xuất xuất hiện trong đề thi tuyển sinh môn Toán lớp 10 theo xu hướng ứng dụng những kiến thức được học vào đời sống. Do vậy việc ôn luyện chủ đề này luôn cần phải được quan tâm, nhất là khi các câu hỏi về toán thực tế luôn ở mức độ vận dụng. Đây là loạt bài viết về dạng toán thực tế để học sinh có thể tìm hiểu và giải những dạng toán này dễ dàng hơn. Ở phần 1 này tôi đưa ra hướng dẫn giải một số bài toán thực tế về dãy số.
Phần 1: Giải quyết một số bài toán thực tế về dãy số
Toán thực tế là một nội dung khá mới mẻ được đề xuất xuất hiện trong đề thi tuyển sinh môn Toán lớp 10 theo xu hướng ứng dụng những kiến thức được học vào đời sống. Do vậy việc ôn luyện chủ đề này luôn cần phải được quan tâm, nhất là khi các câu hỏi về toán thực tế luôn ở mức độ vận dụng. Đây là loạt bài viết về dạng toán thực tế để học sinh có thể tìm hiểu và giải những dạng toán này dễ dàng hơn. Ở phần 1 này Diễn Đàn Máy Tính Cầm Tay đưa ra hướng dẫn giải một số bài toán thực tế về dãy số.
Lưu ý.Trong loạt bài viết này chỉ đưa ra hướng dẫn, không phải lời giải. Các em học sinh không nên trình bày theo, rất dễ bị sót điểm trong kiểm tra.
1. Bài toán thực tế về dãy số
Bài toán thực tế 1. Một cửa hàng có $3$ tấm vải, dài tổng cộng $126m$. Sau khi họ bán đi $\dfrac{1}{2}$ tấm vải thứ nhất, $\dfrac{2}{3}$ tấm vải thứ hai và $\dfrac{3}{4}$ tấm vải thứ ba, thì số vải còn lại ở ba tấm bằng nhau. Hãy tính chiều dài của ba tấm vải lúc ban đầu .
Hướng dẫn
Gọi chiều dài ban đầu của ba tấm vải lần lượt là $a,b,c$.
Ba tấm vải dài tổng cộng $126m\Rightarrow a+b+c=126\,\,\,\,\,\,\left( 1 \right)$
Sau khi họ bán đi $\dfrac{1}{2}$ tấm vải thứ nhất, $\dfrac{2}{3}$ tấm vải thứ hai và $\dfrac{3}{4}$ tấm vải thứ ba, thì số vải còn lại ở ba tấm bằng nhau.
Từ đó ta có:
$(1-\dfrac{1}{2})a=(1-\dfrac{2}{3})b=(1-\dfrac{3}{4})c$
$\Leftrightarrow\dfrac{1}{2}a=\dfrac{1}{3}b=\dfrac{1}{4}c\,\,\,\,\,\,\,\left( 2 \right)$
Từ $\left( 1 \right),\left( 2 \right)$ ta được hệ phương trình $\left\{ \begin{array}{l}a+b+c=126\\3a-2b=0\\2a-c=0\end{array} \right.$
Ta nhập hệ phương trình này vào phương thức phương trình/ hệ phương trình như sau:
Nhập phương trình thứ nhất:
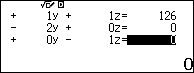
Vậy chiều dài của ba tấm vải lần lượt là $28,42,56$.
Lưu ý. Những bạn nào chưa biết sử dụng phương thức phương trình, hệ phương trình có thể bấm vào đây để hiểu rõ hơn.
Bài toán thực tế 2. Hầu hết vi khuẩn sinh sản bằng cách nhân đôi. Cứ sau $1$ giây, một con vi khuẩn ban đầu sẽ nhân đôi biến thành hai con, thì sau $15$ giây số lượng vi khuẩn là bao nhiêu con?
Hướng dẫn
Ta có: Sau $1$ giây, một con vi khuẩn ban đầu sẽ nhân đôi thành ${{2}^{1}}$ con, sau $2$ giây sẽ thành ${{2}^{2}}$ con. Vậy sau $15$ giây, sẽ thành ${{2}^{15}}=32768$ con.
Bài toán thực tế 3. Ba nhà sản xuất góp vốn theo tỉ lệ là $7; 8; 9$. Hỏi mỗi người nhận được bao nhiêu tiền lãi, biết rằng tổng số tiền lãi là $240$ triệu đồng và tiền lãi chia theo tỉ lệ góp vốn.
Hướng dẫn
Gọi số tiền lãi của từng người lần lượt là $a,b,c$.
Vì số tiền lãi chia theo tỉ lệ góp vốn nên ta có:
$l\left\{ \begin{aligned} & a=\dfrac{7}{7+8+9}.240 \\ & b=\dfrac{8}{7+8+9}.240 \\ & c=\dfrac{9}{7+8+9}.240 \\ \end{aligned} \right.$
Sử dụng phương thức Table để giải quyết
Nhập hàm số:
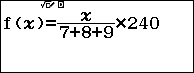
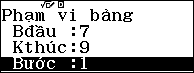
Vậy nên ta có kết quả:$\left\{ \begin{aligned} & a=\dfrac{7}{7+8+9}.240=70 \\ & b=\dfrac{8}{7+8+9}.240=80 \\ & c=\dfrac{9}{7+8+9}.240=90 \\ \end{aligned} \right.$
Lưu ý. Những bạn nào chưa biết sử dụng phương thức Table có thể bấm vào đây để hiểu rõ hơn.
Bài toán thực tế 4. Hùng nói với Mạnh rằng: “Nếu $\Delta ABC$ có $ \widehat{A}:\widehat{B}:\widehat{C}=3:4:5$ thì $\Delta ABC$ là tam giác nhọn.”. Điều Hùng nói có đúng không ? Vì sao ?
Hướng dẫn
Vì $\widehat{A}+\widehat{B}+\widehat{C}=180{}^\circ $ ($A,B,C$ là ba đỉnh của 1 tam giác)
Và $\widehat{A}:\widehat{B}:\widehat{C}=3:4:5$
Nên ta có hệ phương trình:
$\left\{ \begin{array}{l}a+b+c=180\\4a-3b=0\\5a-3c=0\end{array} \right.$
Ta nhập hệ phương trình này vào phương thức phương trình/ hệ phương trình như sau:
Nhập phương trình thứ nhất:
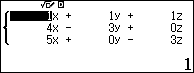
Vậy $\widehat{A}=45{}^\circ ;\widehat{B}=60{}^\circ ;\widehat{C}=75{}^\circ $. Vậy điều Hùng nói là chính xác.
Bài toán thực tế 5. Tìm $3$ số tự nhiên chẵn liên tiếp biết tích hai số sau lớn hơn tích hai số đầu là $480$.
Hướng dẫn
Gọi $3$ số tự nhiên chẵn liên tiếp lần lượt là $2k,2k+2,2k+4\left( k\in \mathbb{N} \right)$.
Ta có: $\left( 2k+4 \right)\left( 2k+2 \right)-\left( 2k+2 \right)\left( 2k \right)=480$
Nhìn vào phương trình trên có vẻ rắc rối, nhưng nếu ta để ý kĩ thì sẽ thấy ta có thể rút được $ 2k+2$ như sau:
$\begin{aligned}& \left( 2k+4 \right)\left( 2k+2 \right)-\left( 2k+2 \right)\left( 2k \right)=480 \\& \Leftrightarrow \left( 2k+2 \right)\left( 2k+4-2k \right)=480 \\& \Leftrightarrow 4\left( 2k+2 \right)=480 \\& \Leftrightarrow 8k+8=480 \\& \Leftrightarrow k=59 \\\end{aligned}$
Xong ta có thể kiểm tra kết quả qua tính năng $Solve$ của máy tính Casio fx-580VNX như sau:
Nhập phương trình vào màn hình như sau:
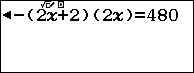
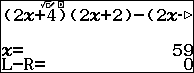
Vậy $k=59$. Và ba số tự nhiên cần tìm là $118,120,122$.
Lưu ý.
- Bạn nào muốn hiểu rõ hơn về tính năng Solve của máy tính Casio fx-580VNX có thể bấm vào đây.
- Ngoài ra, nếu các bạn muốn tìm hiểu thêm về tính năng Solve có thể xem các video trên DIỄN ĐÀN TOÁN CASIO.
————————————–
Đây là loạt bài viết về hướng dẫn giải 1 số bài toán thực tế cấp THCS bằng máy tính cầm tay. Các bạn có góp ý hay bình luận gì cho bài viết này hay muốn ad viết về vấn đề nào thì đừng ngại để lại bình luận hoặc gửi tin nhắn trên fanpage cho ad nhá.
About Bitex Khánh Vũ
