BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Sử dụng tính chất của đường tròn nội tiếp tam giác
- 23/11/2022
- 145 lượt xem
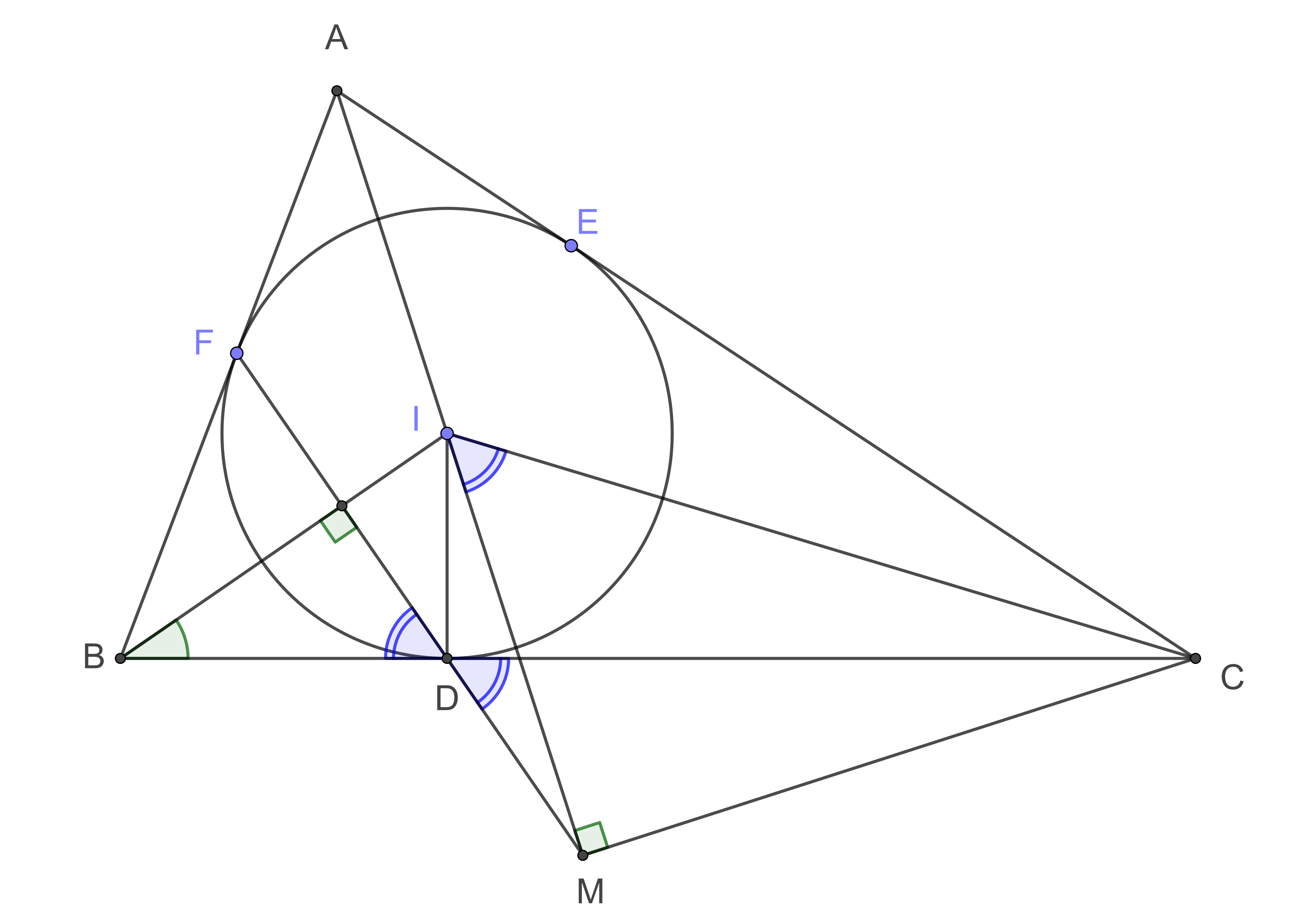
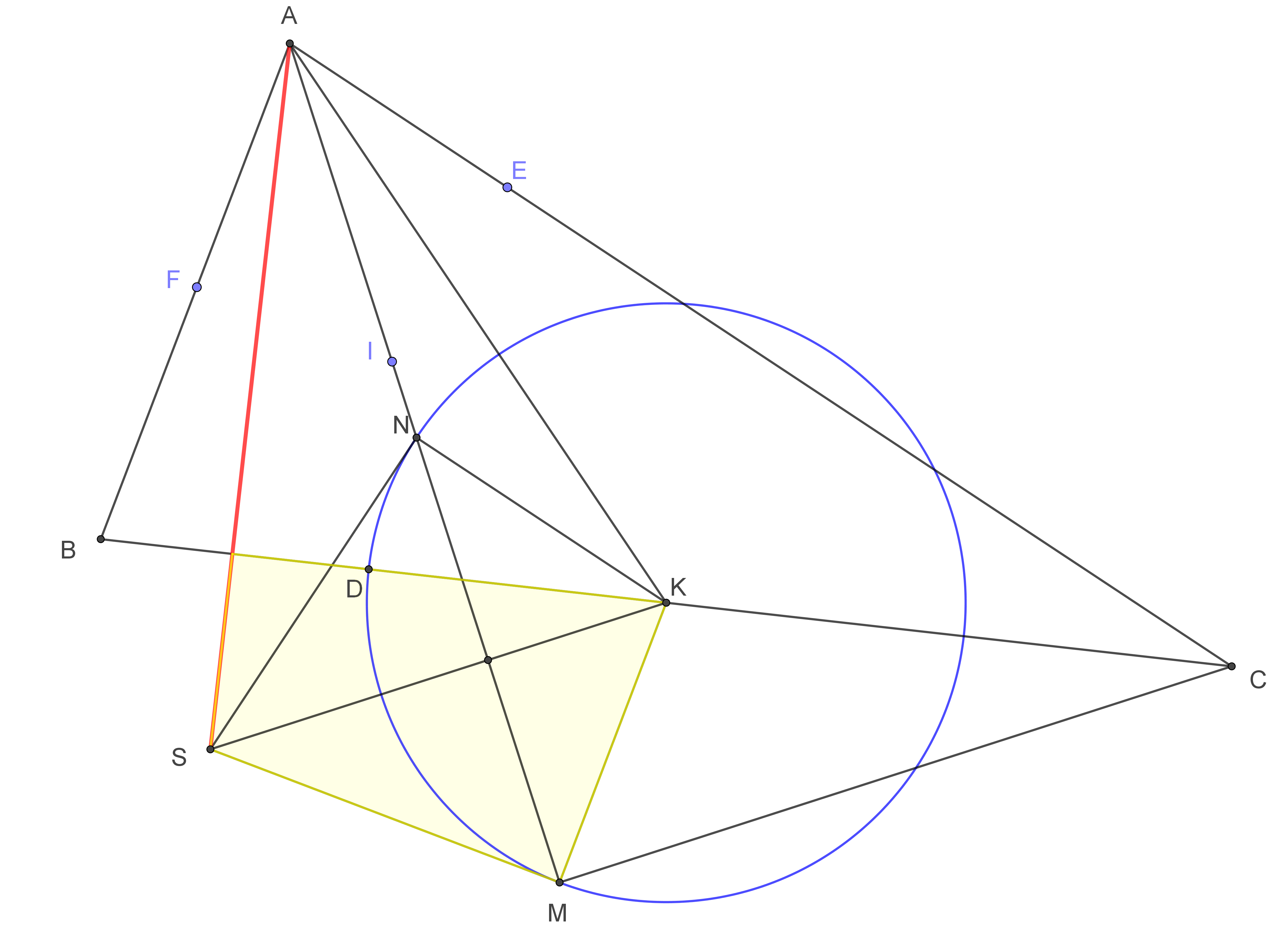
1. Cho tam giác $ABC$. Dựng đường tròn tâm $I$ nội tiếp tam giác và tiếp xúc với ba cạnh $BC, CA, AB$ lần lượt tại $D, E, F$. Gọi $M$ là giao điểm $AI$ và $DF$. Chứng minh $CM\perp AI$.
|
GIẢI: Trong tam giác $AIC$ ta có: $$\widehat{MIC}=\widehat{IAC}+\widehat{ICA}=\dfrac{\widehat{BAC}+\widehat{BCA}}{2}=90^\circ-\dfrac{\widehat{ABC}}{2}=\widehat{FDB}=\widehat{MDC}$$
|
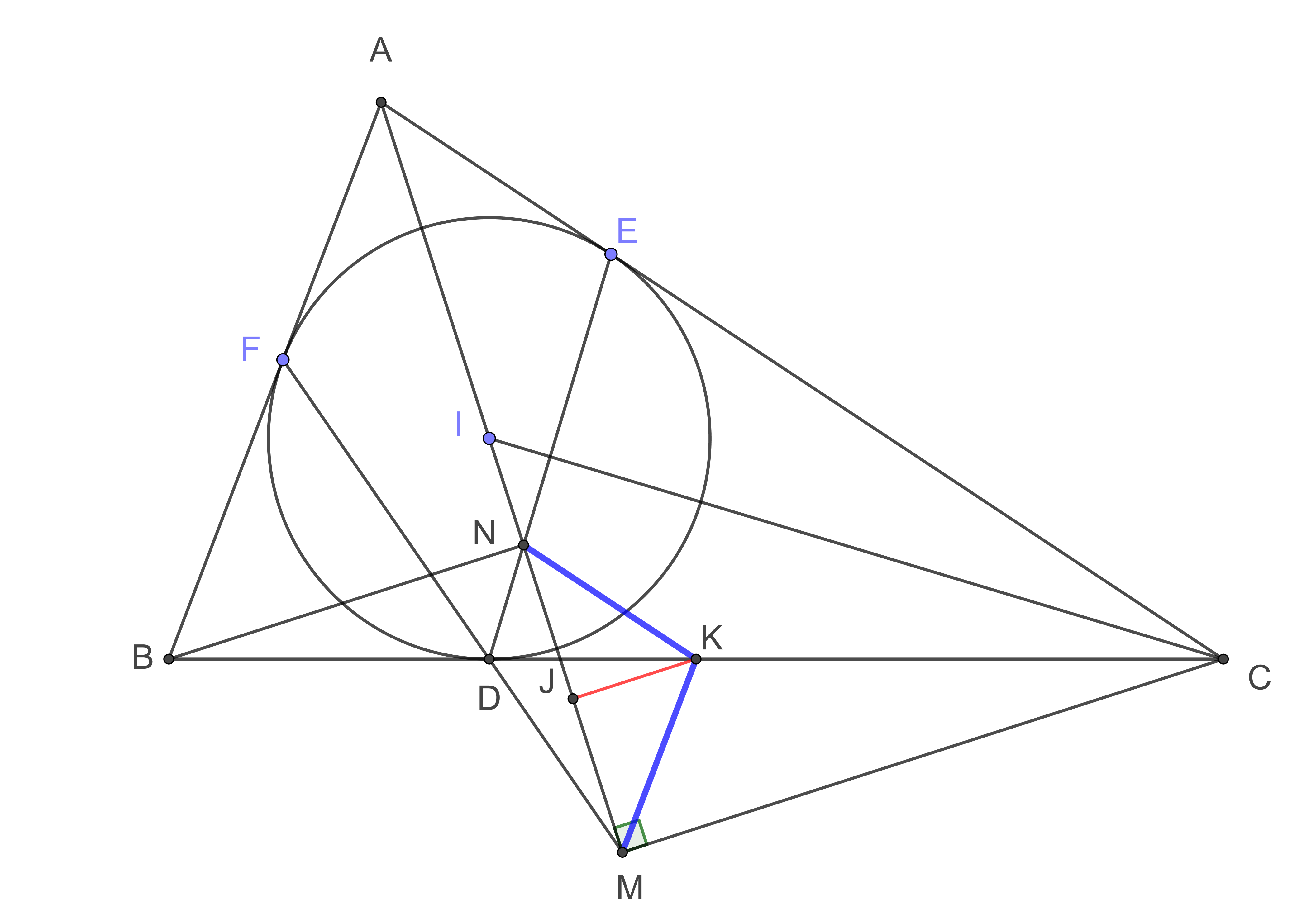
2. Gọi $N$ là giao điểm của $AI$ và $DE$. Gọi $K$ là trung điểm $BC$. Chứng minh $KM=KN.$
|
GIẢI:
Tương tự như trên ta có: $BN\perp AI$. Suy ra $BN/\!/MC$. Vậy $MBNC$ là hình thang. Vì $K$ là trung điểm của đường chéo $BC$ nên nếu ta gọi $J$ là trung điểm của đường chéo $MN$ thì $JK /\!/ MC \Rightarrow KJ\perp MN$. Tam giác $KMN$ có $KJ$ vừa là đường cao vừa là trung tuyến nên tam giác này cân tại $K$ (suy ra đpcm).
|
3. Vẽ đường tròn tâm $K$ bán kính $KM$. Gọi $S$ là giao điểm của các tiếp tuyến tại $M$ và tại $N$ của đường tròn $(K)$. Chứng minh $AS\perp BC.$
|
GIẢI:
Gọi $Q$ là giao điểm của $AS$ và $BC$. Ta chứng minh tứ giác $MSQK$ nội tiếp. Khi đó vì $\widehat{SMK}=90^\circ$ nên suy ra $\widehat{SQK}=90^\circ$. |
About TS. Nguyễn Thái Sơn
