BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Cách phân tích tìm lời giải (bài 1)
- 07/03/2023
- 96 lượt xem
| Bài toán hình học đề thi Toán (chuyên) 2020:
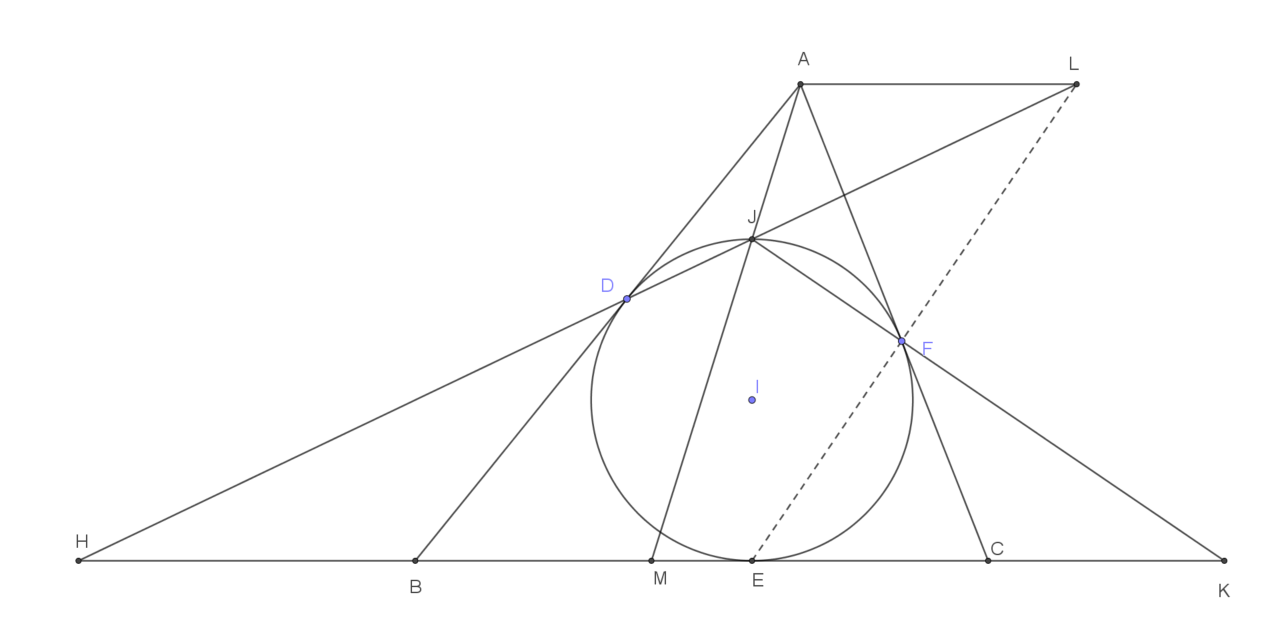
Đường tròn $(I)$ nội tiếp tam giác $ABC$ tiếp xúc với các cạnh $AB, BC, CA$ lần lượt tại $D, E, F$. Kẻ đường kính $EJ$ của đường tròn $(I)$. Gọi $d$ là đường thẳng qua $A$ song song với $BC$. Đường thẳng $JD$ cắt $d$ và $BC$ lần lượt tại $L$ và $H$. a) Chứng minh $E, F, L$ thẳng hàng. b) $JA, JF$ cắt $BC$ lần lượt tại $M, K$. Chứng minh $MH=MK$. |
|
1. Để chứng minh 3 điểm $E, F, L$ thẳng hàng ta có thể chứng minh $\widehat{EFC}=\widehat{AFL}$. Vì ta thấy $\widehat{FCE}=\widehat{FAL}$ (so le trong) nên ta dự đoán $\triangle FCE \backsim \triangle FAL$. Vì tam giác $FCE$ cân tại $C$ nên ta chứng minh tam giác $FAL$ cân tại $A$.
2. Vì ta thấy $AF=AD$ nên ta chứng minh tam giác $ADL$ cân tại $A$. Vì $\widehat{ALD}=\widehat{DHB}$ (so le trong) và $\widehat{ADL}=\widehat{HDB}$ (đối đỉnh) nên $\triangle ADL \backsim BDH$, ta chuyển sang chứng minh tam giác $BDH$ cân tại $B$. 3. Vì tam giác $DHE$ vuông tại $D$ nên ta chỉ cần chứng minh $BD=BE$, điều này là hiển nhiên. |
|
Bài giải câu a
|
Tam giác $JDE$ nội tiếp đường tròn đường kính $JE$ nên là tam giác vuông tại $D$.
Tam giác $HDE$ vuông tại $D$ và có $B$ trên đoạn $HE$ mà $BE=BD$ nên $B$ là trung điểm $HE$.
Vậy tam giác $BHD$ cân tại $B$. Tam giác này đồng dạng với tam giác $ALD$ nên tam giác $ALD$ cận tại $A$.
Vì $AD=AF$ nên tam giác $AFL$ cân tại $A$.
Ngoài ra tam $CFE$ cân tại $C$ và $\widehat{FAL}=\widehat{FCE}$ (so le trong) nên $\triangle AFL \backsim \triangle CFE$ (hai tam giác cân có một góc bằng nhau).
Suy ra $\widehat{AFL}=\widehat{CFE}$ do đó ba điểm $E, F, L$ thẳng hàng (đpcm).
About TS. Nguyễn Thái Sơn
