Cách phân tích tìm lời giải (bài 2)
- 08/03/2023
- 81 lượt xem
| Bài toán (Đề Toán chuyên Hà Nội 2022) |
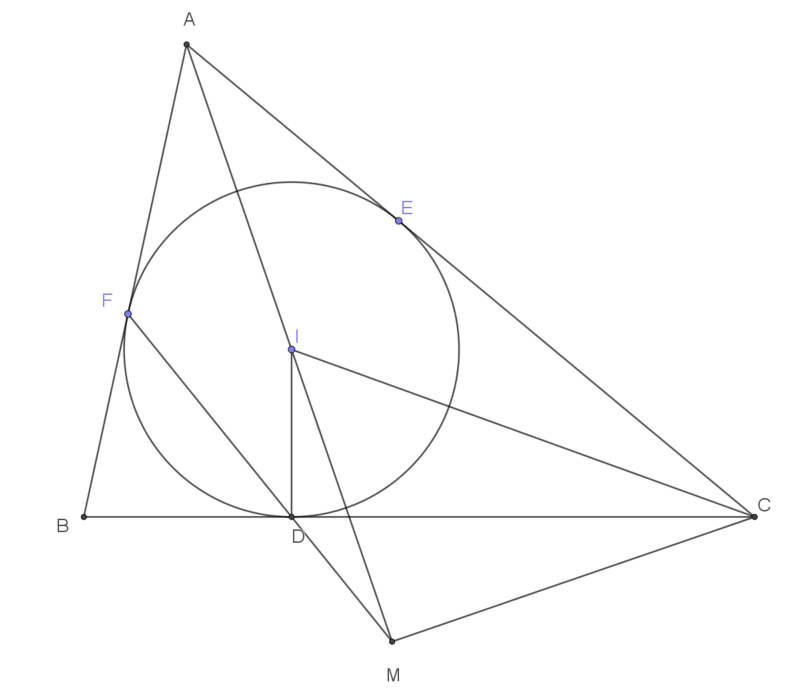
| Cho tam giác $ABC$ ngoại tiếp đường tròn $(I)$, các cạnh $BC, CA, AB$ tiếp xúc với $(I)$ lần lượt tại $D, E, F$. Hai đường thẳng $AI$ và $FD$ cắt nhau tại $M$.
a) Chứng minh $CM \perp AM$. b) Các đường thẳng $ED$ và $AI$ cắt nhau tại $N$. Gọi $K$ là trung điểm $BC$. Chứng minh tam giác $KMN$ là tam giác cân. |
|
Ta có $IB$ là đường phân giác góc $\widehat{ABC}$ và $IB\perp FD$ nên $\widehat{FDB}=90^\circ -\widehat{IBD}= 90^\circ -\dfrac{\widehat{ABC}}{2}$.
Vì $\widehat{MDC}=\widehat{FDB}$ (đối đỉnh) nên $\widehat{MDC}=90^\circ -\dfrac{\widehat{ABC}}{2}\quad (1)$.
Ta có: $\widehat{MIC}=180^\circ-\widehat{AIC}=180^\circ -\left(90^\circ +\dfrac{\widehat{ABC}}{2}\right)= 90^\circ -\dfrac{\widehat{ABC}}{2}\quad (2)$
So sánh (1) và (2) ta suy ra $\widehat{MIC}=\widehat{MDC} ⇒$ tứ giác $IDMC$ nội tiếp. Khi đó $\widehat{CMI}=\widehat{CDI}=90^\circ$ (đpcm)
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay