BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Cách phân tích tìm lời giải (bài 3)
- 09/03/2023
- 93 lượt xem
| Chủ đề của bài này là:
Sử dụng vai trò như nhau của các điểm trong hình vẽ
|
| Trong hình vẽ có hai điểm có vai trò như nhau, ví dụ hai tiếp điểm của hai tiếp tuyến kẻ từ một điểm, nếu điểm này có tính chất gì thì điểm kia cũng có thể có tính chất đó. Khi trình bày lời giải chúng ta chỉ cần nói “chứng minh tương tự “ |
| Áp dụng 1: Bài toán hình học đề thi Toán (chuyên) 2020:
Đường tròn $(I)$ nội tiếp tam giác $ABC$ tiếp xúc với các cạnh $AB, BC, CA$ lần lượt tại $D, E, F$. Kẻ đường kính $EJ$ của đường tròn $(I)$. Gọi $d$ là đường thẳng qua $A$ song song với $BC$. Đường thẳng $JD$ cắt $d$ và $BC$ lần lượt tại $L$ và $H$. a) Chứng minh $E, F, L$ thẳng hàng. b) $JA, JF$ cắt $BC$ lần lượt tại $M, K$. Chứng minh $MH=MK$. |
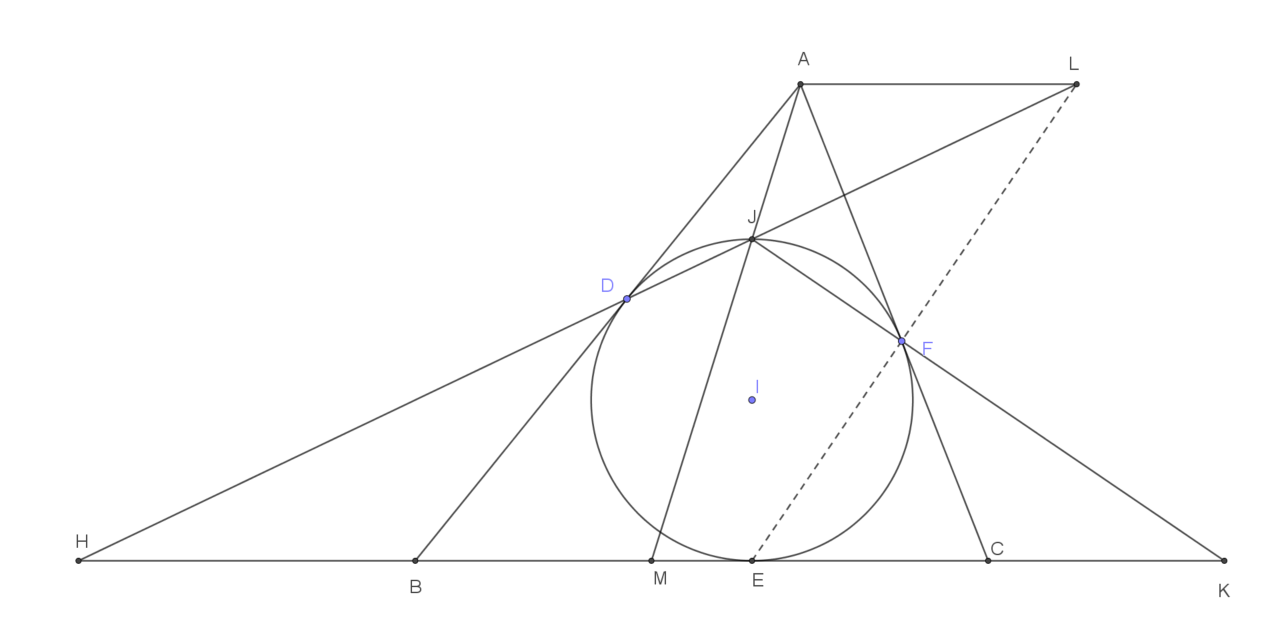
Trong bài phân tích 1 ta đã chứng minh $\triangle ADL$ cân tại $A$ (vì nó đồng dạng với tam giác $BDH$ cân tại $B$).
Nếu ta lấy $A$ là chuẩn thì ta thấy hai tiếp điểm $D$ và $F$ có vai trò như nhau. Vì đường thẳng $DJ$ cắt $d$ tại $L$ (và cắt $BC$ tại $H$) thì ta có $AL=AD$ nên ta dự đoán đường thẳng $FJ$ sẽ cắt $d$ tại $N$ và cắt $BC$ tại $K$ thì ta có $AN=AF$. Sau khi kiểm tra lại dự đoán trên là đúng ta viết vào bài làm là “chứng minh tương tự“.
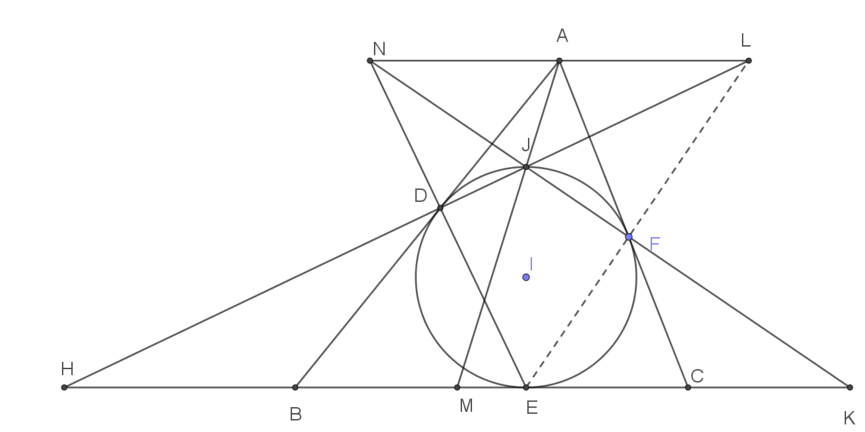
Chứng minh tương tự như câu a ta có tam giác $AFN$ đồng dạng với tam giác cân $CFK$ nên là tam giác cân tại $A$. Vậy $AN=AF=AL$.
Tứ giác $NLKH$ là hình thang, hai đường chéo cắt nhau tại $J$, $A$ là trung điểm $NL$ mà đường thẳng $AJ$ cắt $HK$ tại $M$ nên $M$ là trung điểm $HK$.
| Áp dụng 2: Bài toán (Đề Toán chuyên Hà Nội 2022) |
| Cho tam giác $ABC$ ngoại tiếp đường tròn $(I)$, các cạnh $BC, CA, AB$ tiếp xúc với $(I)$ lần lượt tại $D, E, F$. Hai đường thẳng $AI$ và $FD$ cắt nhau tại $M$.
a) Chứng minh $CM \perp AM$. b) Các đường thẳng $ED$ và $AI$ cắt nhau tại $N$. Gọi $K$ là trung điểm $BC$. Chứng minh tam giác $KMN$ là tam giác cân. |
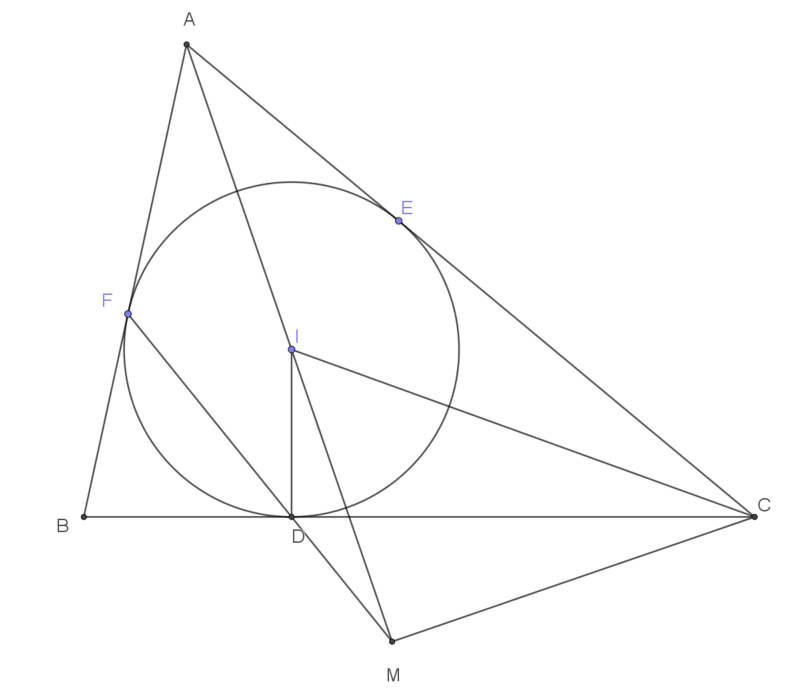
Nếu ta lấy $A$ làm chuẩn thì hai tiếp điểm $E$ và $F$ có vai trò như nhau. Vì đường thẳng $FD$ cắt $AI$ tại $M$ dẫn tới $CM\perp AI$ tại $M$ nên ta dự đoán đường thẳng $ED$ cắt $AI$ tại $N$ dẫn tới $BN\perp AI$ tại $N$. Sau khi kiểm tra dự đoán là đúng ta viết vào bài làm là “chứng minh hoàn toàn tương tự”.
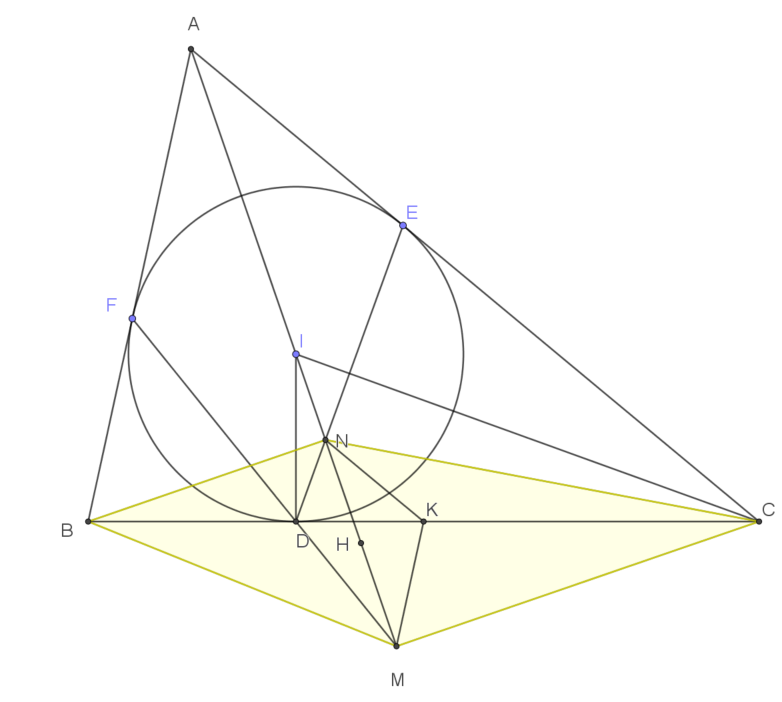
Chứng minh tương tự như câu a ta có $BN\perp AN$.
Suy ra $BN /\!/ MC$ nên tứ giác $BNCM$ là hình thang với hai đường chéo $BC$ và $MN$.
Gọi $H$ là trung điểm của $MN$. Khi đó đoạn nối trung điểm $HK$ của hai đường chéo sẽ song song với hai đáy, nghĩa là $HK /\!/ MC /\!/ BM ⇒ HK\perp AI$, nghĩa là $HK\perp MN$. Tam giác $KMN$ có $KH$ vừa là đường cao vừa là đường trung tuyến nên là tam giác cân tại $K$ (đpcm).
About TS. Nguyễn Thái Sơn
