Một kỹ thuật chứng minh tam giác đồng dạng và áp dụng
- 07/03/2023
- 251 lượt xem
| Giả sử ta có hai tam giác đồng dạng $ABC$ và $A’B’C’$ , các góc tương ứng bằng nhau như hình vẽ: |
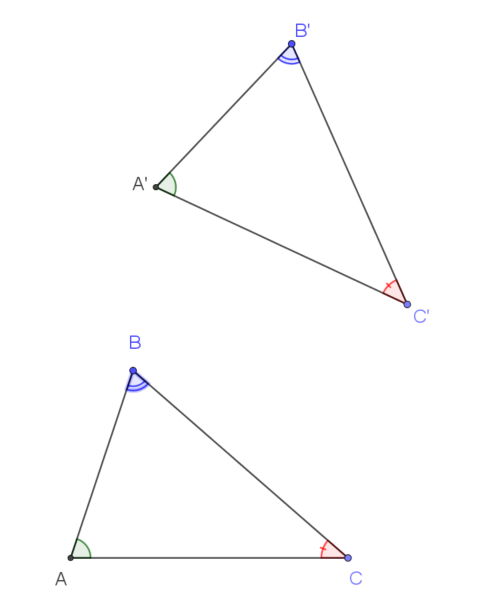
| Lấy $A$ làm tâm vị tự điểm $C$ thành điểm $C_1$ và
lấy $A’$ làm tâm vị tự điểm $C’$ thành điểm $C’_1$ theo cùng tỉ số $k$: |
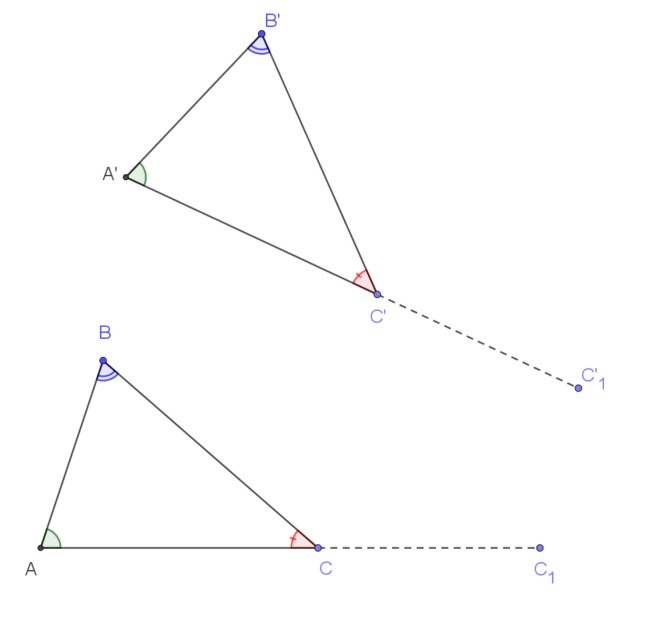
| Khi đó hai tam giác $ABC_1$ và $A’B’C’_1$ nối hai đỉnh cũ và đỉnh mới lập thành hai tam giác đồng dạng. Chú ý hai trường hợp đặc biệt: nếu $k=\dfrac12$: “thu về trung điểm “, nếu $k=2$: “phóng ra gấp đôi “ |
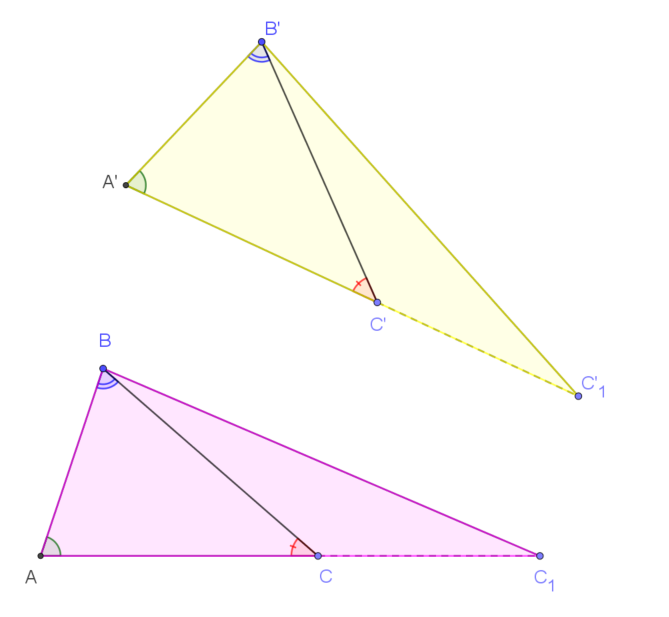
| Chứng minh sự kiện |
Giả sử tam giác $ABC$ đồng dạng với tam giác $A’B’C’$ và $\widehat{A}=\widehat{A’} ; \dfrac{AC}{AB}=\dfrac{A’C’}{A’B’}$
$ ⇒ \dfrac{k.AC}{AB}=\dfrac{k.A’C’}{A’B’} ⇒ \dfrac{AC_1}{AB}=\dfrac{A’C’_1}{A’B’}$.
Hai tam giác $ABC_1$ và $A’B’C’_1$ có: $\widehat{A}=\widehat{A’} ; \dfrac{AC_1}{AB}=\dfrac{A’C’_1}{A’B’}$ nên là hai tam giác đồng dạng.
| Áp dụng: Đề thi Toán chuyên TP HCM năm 2019.
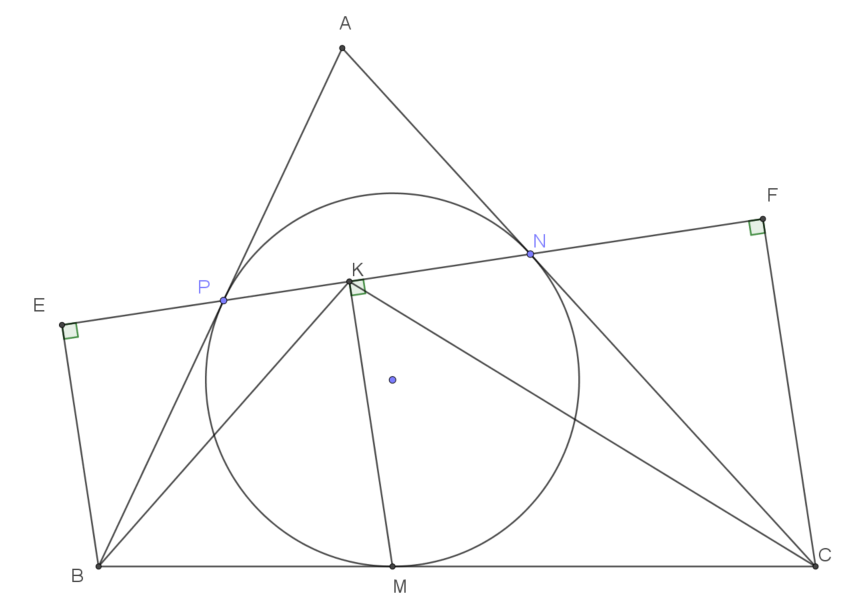
Cho tam giác $ABC$ ngoại tiếp đường tròn $(O)$, các cạnh $BC, CA, AB$ tiếp xúc với đường tròn này lần lượt tại $M, N, P$. Hạ $MK$ vuông góc với $NP$. Chứng minh $KM$ là đường phân giác cúa góc $\widehat{BKC}$. |
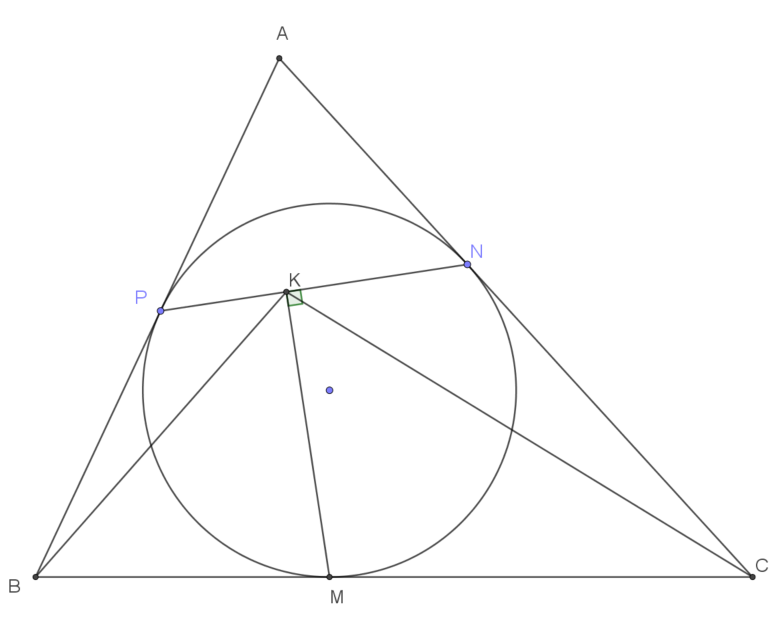
| Phân tích tìm lời giải: |
|
|
Hạ $BE$ và $CF$ vuông góc với đường thẳng $NPP$. Hai tam giác $BPE$ và $CNF$ có:
$$\left\lbrace\begin{array}{l}\widehat{BEP}=\widehat{CFN}=90^\circ\\
\widehat{BPE}=\widehat{CNF}\quad \text{(vì lần lượt đối đỉnh với hai góc bằng nhau}\ \widehat{APN}\ \text{và}\ \widehat{ANP}) \end{array} \right. $$
Suy ra hai tam giác này đồng dạng. Do đó: $\dfrac{PE}{PB}=\dfrac{NF}{NC}\quad (1)$
Áp dụng định lý Thales vào hình thang ta có: $$\dfrac{KE}{KF}=\dfrac{MB}{MC} =\dfrac{PB}{NC} \Leftrightarrow \dfrac{KE}{PB}=\dfrac{KF}{NC}\quad (2)$$
Lấy (2) trừ (1) ta có: $\dfrac{PK}{PB}=\dfrac{NK}{NC}$, ngoài ra $\widehat{BPK}=\widehat{CNK} $ vì lần lượt bù với hai góc bằng nhau $\widehat{BPE}$ và $\widehat{CNF}$ nên $\triangle BPK \backsim \triangle CNK ⇒ \widehat{PKB}=\widehat{NKC} ⇒ \widehat{BKM}=\widehat{CKM}$ (đpcm).
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay