Hệ thống các bài toán BĐT trong các bài thi tuyển sinh 10 của SGD và ĐT Hà Nội trong những năm gần đây

Bài1, bài 2 và bài 3 có chung cách giải như sau:

Bài 1: Đặt $u=a+b, v=ab, u^2\geqslant 4v$.

Ta có: $a^2+b^2=2\Leftrightarrow u^2-2v=2 \Leftrightarrow v=\dfrac{u^2-2}{2}$. Khi đó $P=3u+\dfrac{u^2-2}{2}$.

Điều kiện trở thành $u^2\geqslant 2(u^2-2)\Leftrightarrow u^2\leqslant 4 \Leftrightarrow -2\leqslant u\leqslant 2$.

Ở đây chúng tôi sử dụng MTCT để dự đoán kết quả GTNN của biểu thức $P$ là $-5$.

Trong bài viết sau chúng tôi sẽ hướng dẫn chuyển kết quả dự đoán trên máy tính sang lời giải tự luận để có kết luận hoàn chỉnh.
 
 
Bài 2: Đặt $u=a+b, v=ab, u^2\geqslant 4v$.

Ta có: $a^2+b^2+ab=3\Leftrightarrow (u^2-2v)+v=3 \Leftrightarrow v=u^2-3$. Khi đó $P=(u^4-4u^2v+2v^2)-v=u^4-4u^2(u^2-3)+2(u^2-3)^2-(u^2-3)$.

Thu gọn ta được $P=-u^4-u^2+21$

Điều kiện trở thành $u^2\geqslant 4(u^2-2)\Leftrightarrow u^2\leqslant 4 \Leftrightarrow -2\leqslant u\leqslant 2$.

Ở đây chúng tôi sử dụng MTCT để dự đoán kết quả GTNN của biểu thức $P$ là $1$ và GTLN là $21$.

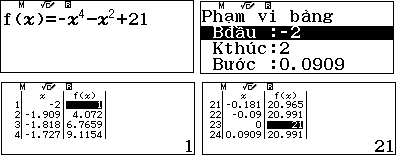
Trong bài viết sau chúng tôi sẽ hướng dẫn chuyển kết quả dự đoán trên máy tính sang lời giải tự luận để có kết luận hoàn chỉnh.
 
 
Bài 3: Đặt $u=x+y, v=xy, u^2\geqslant 4v$.

$x-\sqrt{x+6}=\sqrt{y+6}-y$

$\Leftrightarrow x+y=\sqrt{x+6}+\sqrt{y+6}\quad $ (Điều kiện $u= x+y \geqslant 0$.)

$\Leftrightarrow u^2=u+12+2\sqrt{v+6u+36}$

$\Leftrightarrow u^2-u-12=2\sqrt{v+6u+36}\quad $ (Điều kiện $u^2-u-12\geqslant 0 \Rightarrow u\geqslant 4$.)

$\Leftrightarrow v=\left(\dfrac{u^2-u-12}{2}\right)^2-6u-36$

Điều kiện trở thành $u^2\geqslant (u^2-u-12)^2-24u-144$

Thu gọn biểu thức bằng cách bấm CALC100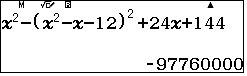

Suy ra $u^4-2u^3-24u^2\leqslant 0 \Leftrightarrow -4\leqslant u\leqslant 6$.

Kết hợp các điều kiện ta có ${\color{blue}4\leqslant u\leqslant 6}$

$u=6\Leftrightarrow v= 9 \Leftrightarrow x=y=3$

$u=4\Leftrightarrow v=-60 \Leftrightarrow x=10, y=-6$ hay $x=-6, y=10$.
 

Vậy GTLN của $x+y$ là 6 và GTNN của $x+y$ là 4.
 
 

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.