BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP NHÂN LIÊN HỢP DƯỚI SỰ HỖ TRỢ CỦA CASIO fx- 580VNX
- 05/04/2022
- 132 lượt xem
Bên cạnh phương pháp NÂNG LŨY THỪA VÀ SỬ DỤNG ĐỊNH LÝ VIET ĐẢO, chúng ta có thể sử dụng phương pháp NHÂN LIÊN HỢP để giải quyết các bài toán giải phương trình vô tỷ. Bài viết này sẽ hướng dẫn bạn đọc cách vận dụng phương pháp nhân liên hợp để giải quyết các bài toán cụ thể dưới sự hỗ trợ của Casio fx 580 vnx.
Bên cạnh phương pháp NÂNG LŨY THỪA VÀ SỬ DỤNG ĐỊNH LÝ VIET ĐẢO, chúng ta có thể sử dụng phương pháp NHÂN LIÊN HỢP để giải quyết các bài toán giải phương trình vô tỷ. Bài viết này sẽ hướng dẫn bạn đọc cách vận dụng phương pháp nhân liên hợp để giải quyết các bài toán cụ thể dưới sự hỗ trợ của Casio fx 580 vnx.
Bài toán 1. Giải phương trình ${{x}^{2}}-x-2=\sqrt{3-x}+\sqrt{x}$
Hướng dẫn giải.
Điều kiện xác định $\left\{ \begin{align}& 3-x\ge 0 \\ & x\ge 0 \\ & {{x}^{2}}-x-2\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & x\le 3 \\ & x\ge 0 \\ & x\le -1,x\ge 2 \\ \end{align} \right.$ $\Leftrightarrow 2\le x\le 3$
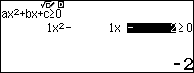
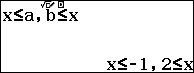
Sử dụng Shift Solve để tìm nghiệm của phương trình ${{x}^{2}}-x-2=\sqrt{3-x}+\sqrt{x}$
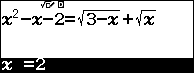
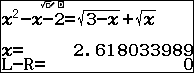
Kiểm tra các căn thức tại nghiệm $x\approx 2.618033989$ ta có: $\left\{ \begin{align} & \sqrt{3-x}\approx 0.6180339887\approx x-2 \\ & \sqrt{x}\approx 1.618033989\approx x-1 \\ \end{align} \right.$
Như vậy các liên hợp chúng ta cần tìm là $\sqrt{3-x}-\left( x-2 \right)$ và $\sqrt{x}-\left( x-1 \right)$
Ta có: ${{x}^{2}}-x-2=\sqrt{3-x}+\sqrt{x}$
$\Leftrightarrow \sqrt{3-x}-\left( x-2 \right)+\sqrt{x}-\left( x-1 \right)-{{x}^{2}}+3x-1=0\\$
$\Leftrightarrow \dfrac{\left( 3-x \right)-{{\left( x-2 \right)}^{2}}}{\sqrt{3-x}+x-2}+\dfrac{x-{{\left( x-1 \right)}^{2}}}{\sqrt{x}+x-1}-{{x}^{2}}+3x-1=0\\$
$\Leftrightarrow \dfrac{-{{x}^{2}}+3x-1}{\sqrt{3-x}+x-2}+\dfrac{-{{x}^{2}}+3x-1}{\sqrt{x}+x-1}-{{x}^{2}}+3x-1=0\\$
$\Leftrightarrow \left( -{{x}^{2}}+3x-1 \right)\left( \dfrac{1}{\sqrt{3-x}+x-2}+\dfrac{1}{\sqrt{x}+x-1}+1 \right)=0\\$
Do $2\le x\le 3$ nên ta có $\left\{ \begin{align} & \sqrt{3-x}+x-2>0 \\ &\sqrt{x}+x-1>0 \\ \end{align} \right.$ , suy ra $\dfrac{1}{\sqrt{3-x}+x-2}+\dfrac{1}{\sqrt{x}+x-1}+1>0$
Như vậy phương trình đã cho tương đương $\left\{ \begin{align} & -{{x}^{2}}+3x-1=0 \\ & 2\le x\le 3 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & x=\dfrac{3\pm \sqrt{5}}{2} \\ & 2\le x\le 3 \\ \end{align} \right.$ $\Leftrightarrow x=\dfrac{3+\sqrt{5}}{2}$
Vậy nghiệm của phương trình là $x=\dfrac{3+\sqrt{5}}{2}$
Bài toán 2. Giải phương trình $\left( 6{{x}^{2}}+12x-6 \right)\sqrt{2x-1}={{x}^{3}}+22{{x}^{2}}-11x$
Hướng dẫn giải
Điều kiện xác định $\left\{ \begin{align} & 2x-1\ge 0 \\ & \left( 6{{x}^{2}}+12x-6 \right)\left( {{x}^{3}}+22{{x}^{2}}-11x \right)\ge 0 \\ \end{align} \right.$
Suy ra$\left\{ \begin{align} & 2x-1\ge 0 \\ & 6{{x}^{2}}+12x-6\ge 0 \\ & {{x}^{3}}+22{{x}^{2}}-11x\ge 0 \\ \end{align} \right.$ $\Rightarrow x\ge \dfrac{1}{2}$
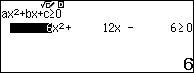
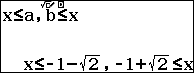
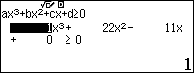
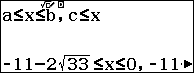
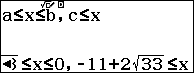
Sử dụng Shift Solve để tìm nghiệm của phương trình $\left( 6{{x}^{2}}+12x-6 \right)\sqrt{2x-1}={{x}^{3}}+22{{x}^{2}}-11x$
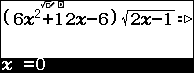
Thay $x=17.48528137$ vào căn thức $\sqrt{2x-1}$ ta được :
$\sqrt{2x-1}\approx 5.828427125\approx \dfrac{x}{3}$ $\Rightarrow x\approx 3\sqrt{2x-1}$
Ta có: $\left( 6{{x}^{2}}+12x-6 \right)\sqrt{2x-1}={{x}^{3}}+22{{x}^{2}}-11x$
$\Leftrightarrow \left( 2{{x}^{2}}+4x-2 \right)3\sqrt{2x-1}={{x}^{3}}+22{{x}^{2}}-11x$
$\Leftrightarrow \left( 2{{x}^{2}}+4x-2 \right)\left( x-3\sqrt{2x-1} \right)={{x}^{3}}-18{{x}^{2}}+9x$
$\Leftrightarrow \left( 2{{x}^{2}}+4x-2 \right)\left( x-3\sqrt{2x-1} \right)=x\left( {{x}^{2}}-18x+9 \right)$
$\Leftrightarrow \left( x-3\sqrt{2x-1} \right)\left( {{x}^{2}}+4x-2-3x\sqrt{2x-1} \right)=0$
Tiếp tục sử dụng Casio fx- 580VNX để tìm nghiệm của phương trình ${{x}^{2}}+4x-2-3x\sqrt{2x-1}=0$
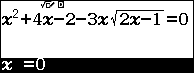
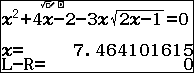
Thay $x=7.464101615$ vào căn thức $\sqrt{2x-1}$ ta được : $\sqrt{2x-1}\approx 3.732050808\approx \dfrac{x}{2}$ $\Rightarrow x\approx 2\sqrt{2x-1}$
Như vậy ta sẽ phân tích ${{x}^{2}}+4x-2-3x\sqrt{2x-1}=0$ như sau:
${{x}^{2}}+4x-2-3x\sqrt{2x-1}=0$$\Leftrightarrow \left( x-2\sqrt{2x-1} \right)\left( x+a\sqrt{2x-1} \right)=0$
Với $a=\dfrac{1}{\sqrt{2x-1}}\left( \dfrac{{{x}^{2}}+4x-2-3x\sqrt{2x-1}}{x-2\sqrt{2x-1}}-x \right)$ $\forall x\in D$
Thay $x=50$ vào biểu thức trên ta tìm được $a=-1$
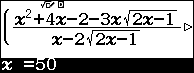
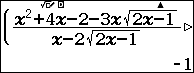
Như vậy ta có: $\left( x-2\sqrt{2x-1} \right)\left( x-\sqrt{2x-1} \right)=0$
Suy ra phương trình đã cho tương đương: $\left( x-3\sqrt{2x-1} \right)\left( x-2\sqrt{2x-1} \right)\left( x-\sqrt{2x-1} \right)=0$
Trường hợp 1. $\left\{ \begin{align} & x-3\sqrt{2x-1}=0 \\ & x\ge \dfrac{1}{2} \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & {{x}^{2}}-18x+9=0 \\ & x\ge \dfrac{1}{2} \\ \end{align} \right.$ $\Leftrightarrow x=9\pm 6\sqrt{2}$
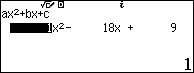
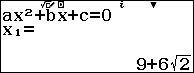
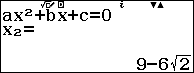
Trường hợp 2. $\left\{ \begin{align} & x-2\sqrt{2x-1}=0 \\ & x\ge \dfrac{1}{2} \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & {{x}^{2}}-8x+4=0 \\ & x\ge \dfrac{1}{2} \\ \end{align} \right.$ $\Leftrightarrow x=4\pm 2\sqrt{3}$
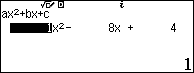
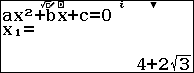
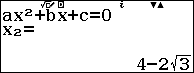
Trường hợp 3. $\left\{ \begin{align} & x-\sqrt{2x-1}=0 \\& x\ge \dfrac{1}{2} \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & {{x}^{2}}-2x+1=0 \\ & x\ge \dfrac{1}{2} \\ \end{align} \right.$ $\Leftrightarrow x=1$
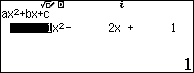
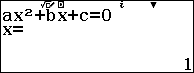
Vậy phương trình có $5$ nghiệm $x=9\pm 6\sqrt{2}$; $x=4\pm 2\sqrt{3}$ và $x=1$
Cảm ơn các bạn đã theo dõi bài viết GIẢI PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP NHÂN LIÊN HỢP DƯỚI SỰ HỖ TRỢ CỦA CASIO fx- 580VNX. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
